当前位置：试卷中心 > 试卷详情

2020-2021学年贵州省遵义市红花岗区八年级（上）期末数学试卷

发布：2024/7/6 8:0:9

一、选择题（本题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满）

1．下列文字中，是轴对称图形的是（　　）
A．我 B．爱 C．中 D．国
组卷：174引用：3难度：0.9
解析
2．新型冠状病毒属于β属的新型冠状病毒，颗粒呈圆形或者椭圆形，直径约60～140纳米（1纳米=10^-9米），某新冠病毒的直径大小是126纳米，用科学记数法可以表示为（　　）
A．12.6×10^-8米 B．1.26×10^-11米
C．1.26×10^-7米 D．126×10^-9米
组卷：6引用：1难度：0.8
解析
3．等腰三角形的两边长为2cm,5cm,则该等腰三角形的周长为（　　）
A．9cm B．12cm C．9cm或12cm D．6cm或12cm
组卷：26引用：2难度：0.6
解析
4．下列各式运算正确的是（　　）
A．a³×a²=a⁶ B．（a²）⁴=a⁸
C．（-a）²+a²=0 D．（2 a³）²=2 a⁶
组卷：11引用：2难度：0.7
解析
5．点A（-2，3）向右平移3个单位后得到点B，那么点B关于x轴对称的点的坐标是（　　）
A．（1，-3） B．（1，3） C．（-1，3） D．（-1，-3）
组卷：7引用：3难度：0.8
解析
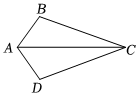6．如图，在△ABC与△ADC中，若∠BAC=∠DAC，则下列条件不能判定△ABC与△ADC全等的是（　　）
A．∠B=∠D B．∠BCA=∠DCA C．BC=DC D．AB=AD
组卷：11引用：1难度：0.7
解析
7．已知（x+m）（x-2）=x²-x-2，那么m的值是（　　）
A．1 B．-1 C．2 D．-2
组卷：9引用：1难度：0.7
解析
8．如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，若AB=20，△ABD的面积为60，则CD长（　　）
A．12 B．10 C．6 D．4
组卷：462引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共8小题，共86分．答题请用0.5毫米黑色墨水签字笔或钢笔书写在答题卡的相应位置上，解答是应写出必要的文字说明，证明过程或演算步骤．）

23．阅读材料：
如图，小明为测量河流宽度，在河岸的一侧选定点B，河的对岸垂直于河岸的方向选定观测目标点A．小明沿点B所在河岸水平向右选取任意点P，继续前行至与BP距离相等处选取点C，再沿与河岸垂直方向行走至点D，使得点D、P、A在同一直线时，测量CD的长即为河流的宽度．
分析：该问题也可以理解为根据BP=CP，即P为BC的中点，过点C作CD∥AB交AP于点D，从而构造了△CDP与△BAP全等，这样的思想是抓住线段的中点，再过线段的一端作平行线，利用平行构造三角形全等，从而解决线段相等问题，也称构造“X”型全等．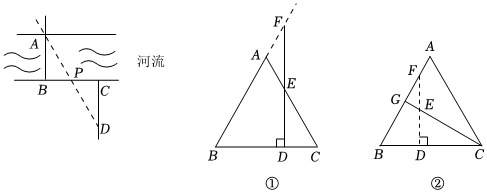

请运用以上模型思想解决以下问题：
等边三角形ABC中，AB=4，点D在BC边上，过点D作DF⊥BC，交射线BA于点F，则
（1）如图①，若DF与AC相交于点E，当EF=ED时，AF与CD有什么数量关系？请说明理由；
（2）如图②，点G是AB边上的中点，连接CG，交DF于点E，EF=ED，求CD的长．
组卷：150引用：2难度：0.4
解析
24．如图1，四边形ABED中，∠B=∠E=∠ACD=90°，BC=DE．
（1）求证：△ABC≌△CED．
（2）发现：若AB=a,BC=b,AC=c,请用两种方法计算四边形ABCD的面积，并探究a、b、c之间有什么数量关系？
（3）应用：
①根据（2）中的发现，当AB=8，BC=6时，AC的长为
；
②如图2，若∠P=30°，PM=4，PN=7，点F在PN上，点G在射线PM上连接FM、FG、NG，求MF+FG+GN的最小值．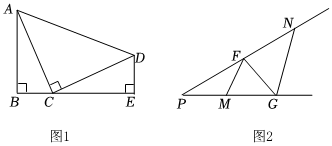
组卷：25引用：2难度：0.1
解析