阅读材料:
如图,小明为测量河流宽度,在河岸的一侧选定点B,河的对岸垂直于河岸的方向选定观测目标点A.小明沿点B所在河岸水平向右选取任意点P,继续前行至与BP距离相等处选取点C,再沿与河岸垂直方向行走至点D,使得点D、P、A在同一直线时,测量CD的长即为河流的宽度.
分析:该问题也可以理解为根据BP=CP,即P为BC的中点,过点C作CD∥AB交AP于点D,从而构造了△CDP与△BAP全等,这样的思想是抓住线段的中点,再过线段的一端作平行线,利用平行构造三角形全等,从而解决线段相等问题,也称构造“X”型全等.
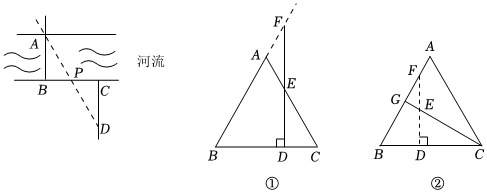
请运用以上模型思想解决以下问题:
等边三角形ABC中,AB=4,点D在BC边上,过点D作DF⊥BC,交射线BA于点F,则
(1)如图①,若DF与AC相交于点E,当EF=ED时,AF与CD有什么数量关系?请说明理由;
(2)如图②,点G是AB边上的中点,连接CG,交DF于点E,EF=ED,求CD的长.
【答案】(1)AF=CD,理由见解析;
(2)CD=.
(2)CD=
12
5
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/6 8:0:9组卷:170引用:2难度:0.4
相似题
-
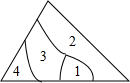 1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第块.发布:2025/6/23 17:0:1组卷:2707引用:48难度:0.7
1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第块.发布:2025/6/23 17:0:1组卷:2707引用:48难度:0.7 -
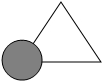 2.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )发布:2025/6/24 13:0:11组卷:2137引用:137难度:0.9
2.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )发布:2025/6/24 13:0:11组卷:2137引用:137难度:0.9 -
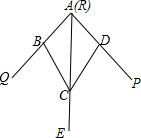 3.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )发布:2025/6/23 18:0:2组卷:5749引用:83难度:0.9
3.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )发布:2025/6/23 18:0:2组卷:5749引用:83难度:0.9


