2022-2023学年福建省福州一中高三（上）第一次调研数学试卷

一、选择题；本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x|y=lg（x+3）}，B={x|x≥2}，则下列结论正确的是（　　）

  A．-3∈A

  B．3∉B

  C．A∩B=B

  D．A∪B=B
  组卷：27引用：6难度：0.9

  解析

• 2．如果复数（m²-3m）+（m²-5m+6）i是纯虚数，则实数m的值为（　　）

  A．0

  B．2

  C．0或3

  D．2或3
  组卷：45引用：21难度：0.9

  解析

• 3．若函数f（x）同时满足：
  （1）对于定义域内的任意x,有f（x）+f（-x）=0；
  （2）对于定义域内的任意x₁，x₂，当x₁≠x₂时，有

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ＜

  0

  ，则称函数f（x）为“理想函数”．
  给出下列四个函数：①f（x）=x²；②f（x）=-x³；③

  f

  （

  x

  ）

  =

  x

  -

  1

  x

  ；④

  f

  （

  x

  ）

  =

  - x 2 ， x ≥ 0

  x 2 ， x ＜ 0

  ．
  其中是“理想函数”的序号是（　　）

  A．①②

  B．②③

  C．②④

  D．③④
  组卷：108引用：4难度：0.5

  解析

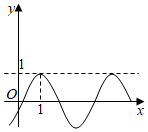• 4．已知函数f（x）=cos（ωx-φ）（0＜ω＜4，0＜φ＜π）的部分图象如图所示，f（0）=cos2，则下列判断正确的是（　　）

  A．函数f（x）的最小正周期为4

  B．函数f（x）的图象关于直线x=6π-1对称

  C．函数f（x）的图象关于点（ π 4 +1，0）对称

  D．函数f（x）的图象向左平移2个单位得到一个偶函数的图象
  组卷：134引用：9难度：0.6

  解析

• 5．设a,b,c都是正数，且4^a=6^b=9^c，则下列结论错误的是（　　）

  A．c＜b＜a	B．ab+bc=ac
  C．4b•9b=4a•9c	D． 1 c = 2 b - 1 a
  组卷：171引用：3难度：0.6

  解析

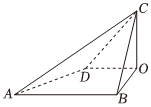• 6．如图，在四棱锥C-ABOD中，CO⊥平面ABOD，AB∥OD，OB⊥OD，且AB=2OD=12，

  AD

  =

  6

  2

  ，异面直线CD与AB所成角为30°，点O，B，C，D都在同一个球面上，则该球的表面积为（　　）

  A．21π

  B．42π

  C．48π

  D．84π
  组卷：99引用：5难度：0.5

  解析

• 7．已知sin（2α-β）=-3sinβ，且α-β≠

  π

  2

  +kπ，α≠

  kπ

  2

  ，其中k∈Z，则

  tan

  （

  α

  -

  β

  ）

  tanα

  =（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：193引用：7难度：0.7

  解析

四、解答题；本题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤．

• 21．已知各项均为正数的两个数列{a_n}，{b_n}满足a_n+1²-1=a_n²+2a_n，2a_n=log₂b_n+log₂b_n+1+1，且a₁=b₁=1．
  （1）求证：数列{a_n}为等差数列；
  （2）求数列{b_n}的通项公式；
  （3）设数列{a_n}，{b_n}的前n项和分别为S_n，T_n，求使得等式2S_m+a_m-36=T_i成立的有序数对（m,i）（m,i∈N*）．
  组卷：188引用：4难度：0.3

  解析

• 22．已知函数f（x）=ax³+bx+2在x=-2处取得极值-14．
  （1）求a,b的值；
  （2）求曲线y=f（x）在点（1，f（1））处的切线方程；
  （3）求函数f（x）在[-3，3]上的最值．
  组卷：106引用：16难度：0.4

  解析