2022-2023学年湖南省株洲市炎陵县高一（下）期末数学试卷

一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合U={1，2，3，4，5}，A={1，3}，B={1，2，4}，则（∁_UB）∪A=（　　）

  A．{1，3，5}

  B．{1，3}

  C．{1，2，4}

  D．{1，2，4，5}
  组卷：1282引用：11难度：0.7

  解析

• 2．若向量

  a

  、

  b

  满足|

  a

  |=|

  b

  |=1，且

  a

  与

  b

  的夹角为60°，则

  a

  •

  a

  -

  a

  •

  b

  等于（　　）

  A． 1 2

  B． 3 2

  C． - 1 2

  D．- 3 2
  组卷：51引用：3难度：0.7

  解析

• 3．在正方体ABCD-A₁B₁C₁D₁中，E，F分别为AB，AD的中点，则异面直线B₁C与EF所成角的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：40引用：4难度：0.7

  解析

• 4．在空间中给出下列命题：（1）垂直于同一直线的两直线平行．（2）两条直线没有公共点，则这两条直线平行．（3）平行于同一直线的两直线平行．（4）垂直于同一平面的两直线平行．其中正确的命题个数是（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：13引用：2难度：0.5

  解析

• 5．若

  z

  =

  a

  +

  i

  1

  -

  i

  （

  a

  ∈

  R

  ）

  是纯虚数，则a=（　　）

  A． - 1 2

  B． 1 2

  C．-1

  D．1
  组卷：65引用：5难度：0.8

  解析

• 6．已知

  a

  =

  （

  1

  ，

  m

  ）

  与

  b

  =

  （

  n

  ,-

  4

  ）

  共线，且向量

  b

  与向量

  c

  =

  （

  2

  ，

  3

  ）

  垂直，则m+n=（　　）

  A． 15 2

  B． 16 3

  C． - 10 3

  D．-2
  组卷：74引用：5难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  lo g 2 x , x ＞ 0

  - sinx , x ≤ 0

  ，则

  f

  （

  f

  （

  -

  π

  6

  ）

  ）

  =（　　）

  A． 2

  B．1

  C．-1

  D．2
  组卷：67引用：6难度：0.7

  解析

四、解答题（本题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤）

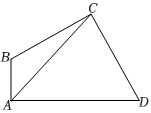• 21．如图，在平面四边形ABCD中，AB⊥AD，

  ∠

  ABC

  =

  2

  3

  π

  ，AB=1．
  （1）若

  AC

  =

  7

  ，求△ABC的面积；
  （2）若

  ∠

  ADC

  =

  π

  3

  ，

  CD

  =

  2

  3

  ，求tan∠CAD．
  组卷：650引用：11难度：0.5

  解析

• 22．已知函数y=f（x），若存在实数m、k（m≠0），使得对于定义域内的任意实数x,均有m•f（x）=f（x+k）+f（x-k）成立，则称函数f（x）为“可平衡”函数；有序数对（m,k）称为函数f（x）的“平衡”数对．
  （1）若f（x）=x²，求函数f（x）的“平衡”数对；
  （2）若m=1，判断f（x）=sinx是否为“可平衡”函数，并说明理由；
  （3）若m₁、m₂∈R，且

  （

  m

  1

  ，

  π

  2

  ）

  、

  （

  m

  2

  ，

  π

  4

  ）

  均为函数

  f

  （

  x

  ）

  =

  co

  s

  2

  x

  （

  0

  ＜

  x

  ≤

  π

  4

  ）

  的“平衡”数对，求

  m

  2

  1

  +

  m

  2

  2

  的取值范围．
  组卷：46引用：14难度：0.6

  解析