2023-2024学年湖北省部分名校新起点高三(上)联考数学试卷(8月份)
发布:2024/8/12 1:0:1
一、选择题:共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x|2x<4},B={x|x2-5x-6<0},则A∪B=( )
组卷:30引用:2难度:0.8 -
2.已知复数z满足zi+3=2i,则
=( )|z-i|组卷:42引用:4难度:0.7 -
3.已知向量
,向量a=(1,2),b=(1,1)满足c,a∥c,则(a+c)∥b=( )|c|组卷:68引用:2难度:0.8 -
4.下列函数
中,函数值域与函数f1(x)=sin2x+1sin2x,f2(x)=x+1x,f3(x)=ex+1ex,f4(x)=lnx+1lnx的值域完全相同的有( )f(x)=x+1x组卷:59引用:2难度:0.5 -
5.等差数列{an}中,Sn是数列{an}的前n项和,e是自然对数的底数,若
,则ea3•ea9=4=( )eS11组卷:49引用:3难度:0.8 -
6.已知
,若α∈(0,π2),则sin(α-π6)=45=( )cos(π6-2α)组卷:79引用:2难度:0.8 -
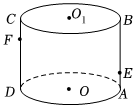 7.如图,已知圆柱底面半径为2,高为3,矩形ABCD是轴截面,E,F分别是母线AB,CD上的动点(含端点),过EF与轴截面ABCD垂直的平面与圆柱侧面的交线是圆或椭圆,当此交线是椭圆时,其离心率的取值范围是( )组卷:100引用:5难度:0.5
7.如图,已知圆柱底面半径为2,高为3,矩形ABCD是轴截面,E,F分别是母线AB,CD上的动点(含端点),过EF与轴截面ABCD垂直的平面与圆柱侧面的交线是圆或椭圆,当此交线是椭圆时,其离心率的取值范围是( )组卷:100引用:5难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数f(x)=xex,g(x)=x2+2x+m.
(1)设函数F(x)=f(x)+g(x),且对∀x,F(x)≥-1成立,求m的最小值;
(2)若函数y=f(x)的图像上存在一点P与函数的图像上一点Q关于x轴对称,求|PQ|的长.h(x)=lnxx组卷:46引用:3难度:0.4 -
22.直角坐标系xOy中,已知动点P到定点
的距离比动点P到定直线F(0,14)的距离小1,记动点P的轨迹为C.y=-54
(1)求轨迹C的方程;
(2)点S,T是曲线C上位于直线的上方的点,过点S,T作曲线C的切线交于点Q,若FS⊥FT,证明:cos∠SQT为定值.y=14组卷:63引用:2难度:0.5


