2022-2023学年北京市大兴区高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目

• 1．复数（1+i）²=（　　）

  A．0

  B．2

  C．2i

  D．-2i
  组卷：34引用：1难度：0.8

  解析

• 2．已知向量

  a

  =（1，-2）与

  b

  =（2，m），且

  b

  =2

  a

  ，则m=（　　）

  A．-4

  B．-1

  C．1

  D．4
  组卷：129引用：1难度：0.8

  解析

• 3．某学校现有小学和初中学生共2000人，为了解学生的体质健康合格情况，决定采用分层抽样的方法从全校学生中抽取一个容量为400的样本，其中被抽到的初中学生人数为180，那么这所学校的初中学生人数为（　　）

  A．800

  B．900

  C．1000

  D．1100
  组卷：72引用：1难度：0.8

  解析

• 4．已知在复平面内复数z对应的点的坐标为（-3，4），则|

  z

  |=（　　）

  A．3

  B．4

  C．5

  D． 4 2
  组卷：44引用：2难度：0.7

  解析

• 5．已知平面α，β，直线l⊂α，则“l∥β”是“α∥β”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：95引用：2难度：0.7

  解析

• 6．设

  a

  ，

  b

  为非零向量，且满足|

  a

  +

  b

  |=|

  a

  -

  b

  |，则

  a

  •

  b

  =（　　）

  A．0

  B．-1

  C．1

  D． 2
  组卷：131引用：1难度：0.8

  解析

• 7．在△ABC中，a=3，b-c=2，

  cos

  B

  =

  -

  1

  2

  ，则b=（　　）

  A． 7

  B． 2 7

  C．5

  D．7
  组卷：235引用：1难度：0.8

  解析

三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。

• 20．在△ABC中，a²+c²-b²=ac,D是AC边上的点，CD=1，AD=BD=3．
  （Ⅰ）求B的大小；
  （Ⅱ）求tanA的值；
  （Ⅲ）求△BCD的面积．
  组卷：95引用：1难度：0.6

  解析

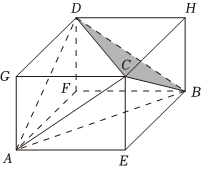• 21．如图，从长、宽、高分别为a,b,c的长方体AEBF-GCHD中截去部分几何体后，所得几何体为三棱锥A-BCD．
  （Ⅰ）求三棱锥A-BCD的体积；
  （Ⅱ）证明：三棱锥A-BCD的每个面都是锐角三角形；
  （Ⅲ）直接写出一组a,b,c的值，使得二面角D-AB-C是直二面角．
  组卷：119引用：3难度：0.6

  解析