2023-2024学年北京十七中高三(上)月考数学试卷(10月份)
发布:2024/9/5 5:0:8
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
-
1.已知集合A={x∈Z|x2<4},B={-1,2},则A∪B=( )
组卷:244引用:6难度:0.9 -
2.已知命题:∀x∈(0,+∞),x2>x.该命题的的否定是( )
组卷:20引用:1难度:0.8 -
3.已知
,且α∈(π2,3π2),那么sinα=( )tanα=2组卷:330引用:10难度:0.8 -
4.下列函数中,在定义域上为奇函数,并且在区间(0,+∞)上是减函数的是( )
组卷:86引用:5难度:0.7 -
5.已知对∀x∈(0,+∞),不等式
恒成立,则实数m的最大值是( )x>m-1x组卷:107引用:3难度:0.5 -
6.已知等比数列{an}的公比为q,则“q>1”是“an-an+1<0”的( )
组卷:83引用:4难度:0.7 -
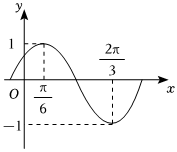 7.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,则( )(ω>0,|φ|<π2)组卷:230引用:4难度:0.5
7.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,则( )(ω>0,|φ|<π2)组卷:230引用:4难度:0.5
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
-
20.已知函数f(x)=2sinx-xcosx-ax(a∈R).
(Ⅰ)若曲线y=f(x)在点(0,f(0))处的切线的斜率为1.
(i)求a的值;
(ii)证明:函数f(x)在区间(0,π)内有唯一极值点;
(Ⅱ)当a≤1时,证明:对任意x∈(0,π),f(x)>0.组卷:634引用:3难度:0.3 -
21.已知项数为k(k≥3)的数列{an}是各项均为非负实数的递增数列.若对任意的i,j(1≤i≤j≤k),aj+ai与aj-ai至少有一个是数列{an}中的项,则称数列{an}具有性质ℜ.
(Ⅰ)判断数列0,1,4,6是否具有性质ℜ,并说明理由;
(Ⅱ)设数列{an}具有性质ℜ,求证:2(a1+a2+⋯+ak-1+ak)=kak;
(Ⅲ)若数列{an}具有性质ℜ,且{an}不是等差数列,求项数k的所有可能取值.组卷:90引用:3难度:0.3


