当前位置：试卷中心 > 试卷详情

2022-2023学年广东省江门市开平市高二（上）期中数学试卷

发布：2024/9/29 0:0:1

1．在空间四边形OABC中，
OA
+
AB
+
BC
等于（　　）
A．
OA
B．
AB
C．
OC
D．
AC
组卷：35引用：9难度：0.9
解析
2．直线
x
-
3
y
-
1
=
0
的倾斜角α=（　　）
A．30° B．60° C．120° D．150°
组卷：79引用：5难度：0.9
解析
3．两条直线l₁：2x-y-1=0与l₂：x+3y-11=0的交点坐标为（　　）
A．（3，2） B．（2，3） C．（-2，-3） D．（-3，-2）
组卷：158引用：4难度：0.7
解析
4．直线x-y+4=0与圆x²+y²=r²相切，则r的值是（　　）
A．
2
2
B．2 C．
2
D．
2
2
组卷：30引用：5难度：0.8
解析
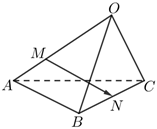5．如图所示，空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在OA上，且
OM
=
2
MA
，N为BC中点，则
MN
等于（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．
-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
2
3
c
D．
2
3
a
+
2
3
b
-
1
2
c
组卷：322引用：25难度：0.7
解析
6．已知圆C的一条直径的端点坐标分别是（4，1）和（-2，3），则圆C的方程是（　　）
A．（x+1）²+（y+2）²=10 B．（x-1）²+（y-2）²=40
C．（x-1）²+（y-2）²=10 D．（x+1）²+（y+2）²=40
组卷：185引用：3难度：0.7
解析
7．已知x,y∈R，向量
a
=
（
x
,
1
，
1
）
，
b
=
（
1
，
y
,
1
）
，
c
=
（
3
，-
6
，
3
）
，且
a
⊥
c
，
b
∥
c
，则
|
a
+
b
|
=（　　）
A．
2
2
B．
2
3
C．4 D．3
组卷：588引用：25难度：0.7
解析

21．如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面A₁B₁C₁，AC⊥AB，AC=AB=4，AA₁=6，点E，F分别为CA₁与AB的中点．
（1）证明：EF∥平面BCC₁B₁．
（2）求B₁F与平面AEF所成角的正弦值．
组卷：336引用：13难度：0.7
解析
22．如图，已知四棱锥P-ABCD，底面ABCD是边长为4的菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
（Ⅰ）求证：AE⊥PD；
（Ⅱ）若PA=4，求二面角E-AF-C的余弦值．
组卷：126引用：3难度：0.5
解析

A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
C． 1 2 a + 1 2 b - 2 3 c	D． 2 3 a + 2 3 b - 1 2 c

A．（x+1）²+（y+2）²=10	B．（x-1）²+（y-2）²=40
C．（x-1）²+（y-2）²=10	D．（x+1）²+（y+2）²=40

1．在空间四边形OABC中，OA+AB+BC等于（ ）