2022-2023学年海南师大附中八年级（下）期末数学试卷

一、选择题（每小题3分，共36分）

• 1．要使二次根式

  x

  -

  3

  有意义，则x的值可以为（　　）

  A．0

  B．1

  C．2

  D．4
  组卷：1027引用：36难度：0.9

  解析

• 2．《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并做出明确规定．某班有7名学生已经学会炒的菜品的种数依次为：3，5，4，6，3，3，4．则这组数据的众数和中位数分别是（　　）

  A．3，4

  B．4，3

  C．3，3

  D．4，4
  组卷：821引用：21难度：0.9

  解析

• 3．一次函数y=-5x+3的图象经过的象限是（　　）

  A．一，二，三

  B．二，三，四

  C．一，二，四

  D．一，三，四
  组卷：1421引用：64难度：0.9

  解析

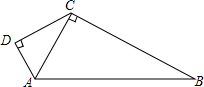• 4．如图，AD⊥CD，CD=4，AD=3，∠ACB=90°，AB=13，则BC的长是（　　）

  A．8

  B．10

  C．12

  D．16
  组卷：633引用：6难度：0.7

  解析

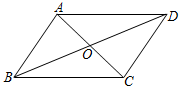• 5．在下列给出的条件中，能判定四边形ABCD为平行四边形的是（　　）

  A．AB∥CD，AD=BC	B．∠BAD=∠ABC，∠BCD=∠ADC
  C．AB=AD，CB=CD	D．AO=OC，DO=OB
  组卷：433引用：3难度：0.5

  解析

• 6．如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为CD的中点．若OE=3，则菱形ABCD的周长为（　　）

  A．6

  B．12

  C．24

  D．48
  组卷：2495引用：24难度：0.7

  解析

• 7．某校规定学生的体育成绩由三部分组成，早锻炼及体育课外活动表现占成绩的20%，体育理论测试占30%，体育技能测试占50%，小颖的上述三项成绩依次是91分、86分、96分，则小颖这学期的体育成绩是（　　）

  A．89分

  B．90分

  C．91分

  D．92分
  组卷：229引用：3难度：0.7

  解析

• 8．已知一次函数y=kx+b的图象经过点（1，-1）和（2，1），那么此一次函数的解析式为（　　）

  A．y=x-2

  B．y=2x-3

  C．y=-x+1

  D．y=-x-1
  组卷：292引用：1难度：0.7

  解析

三、解答题（满分66分）

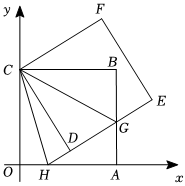• 23．如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形OCBA绕点C逆时针旋转角度一个锐角度数α，得到正方形DCFE，ED交线段AB与点G，ED的延长线交线段OA于点H，连CH、CG．
  （1）求证：△CBG≌△CDG；
  （2）认真探究，求出∠HCG的度数；猜想HG、OH、BG之间的数量关系，并写出理由．
  （3）连接BD、DA、AE、EB得到四边形AEBD，在旋转过程中四边形AEBD能否为矩形？如果能，请求出点H的坐标；如果不能，请说明理由．
  组卷：27引用：2难度：0.1

  解析

• 24．如图，已知抛物线y=x²+bx+c经过点A（-1，-1）和点B（4，4）．
  （1）求该抛物线的解析式；
  （2）点P是抛物线上的一动点（点P在直线AB的下方），过点P作PQ∥y轴，交直线AB于点Q．设点P的横坐标为m,求线段PQ的长（用含m的代数式表示）；
  （3）在（2）的条件下，连接PA、PB，求△PAB面积的最大值，并求出此时点P的坐标．
  组卷：1011引用：7难度：0.5

  解析