2022-2023学年山东省淄博市高二（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知f（x）=x²+2xf′（1），则f′（1）等于（　　）

  A．0

  B．-4

  C．-2

  D．2
  组卷：303引用：7难度：0.9

  解析

• 2．已知等差数列{a_n}的前n项和为S_n，a₂+a₈=10，则S₉-a₅=（　　）

  A．25

  B．40

  C．45

  D．80
  组卷：95引用：3难度：0.7

  解析

• 3．某市高二年级进行了一次教学质量检测，考生共2万人，经统计分析数学成绩服从正态分布，其平均分为85分，60分以下的人数约15%，则数学成绩在85分至110分之间的考生人数约为（　　）

  A．3000

  B．5000

  C．7000

  D．14000
  组卷：22引用：2难度：0.7

  解析

• 4．某医院要安排5名医生到A、B、C三个社区参加义诊，每位医生必须去一个社区，每个社区至少有一名医生．则不同的安排方法数为（　　）

  A．150

  B．210

  C．240

  D．180
  组卷：36引用：2难度：0.7

  解析

• 5．已知

  （

  x

  2

  +

  1

  x

  ）

  n

  的展开式中第三项与第四项的系数之比为

  1

  2

  ，则其展开式中二项式系数最大的项为（　　）

  A．第3项

  B．第4项

  C．第5项

  D．第6项
  组卷：80引用：4难度：0.5

  解析

• 6．意大利数学家斐波那契在1202年著的《计算之书》中记载了斐波那契数列{F_n}，此数列满足：F₁=F₂=1，且从第三项开始，每一项都是它的前两项的和，即

  F

  n

  +

  2

  =

  F

  n

  +

  1

  +

  F

  n

  （

  n

  ∈

  N

  *

  ）

  ，则在该数列的前2023项中，奇数的个数为（　　）

  A．672

  B．675

  C．1349

  D．2022
  组卷：59引用：2难度：0.8

  解析

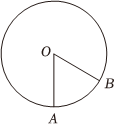• 7．如图，圆O的半径为1，从中剪出扇形AOB围成一个圆锥（无底），所得的圆锥的体积的最大值为（　　）

  A． 2 4 π

  B． 2 12 π

  C． 4 9 3 π

  D． 2 3 27 π
  组卷：98引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．记S_n为数列{a_n}的前n项和，b_n为数列{S_n}的前n项积，已知

  2

  S

  n

  +

  1

  b

  n

  =2．
  （1）证明：数列{b_n}是等差数列；
  （2）求{a_n}的通项公式．
  组卷：14009引用：15难度：0.5

  解析

• 22．已知函数f（x）=2sinx-ln（1+x）（0＜x＜π）．
  （1）证明：函数f（x）有唯一的极值点α，及唯一的零点β；
  （2）对于（1）问中α，β，比较2α与β的大小，并证明你的结论．
  组卷：22引用：1难度：0.5

  解析