2022-2023学年湖南省张家界市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知z=2-i,则z（

  z

  +i）=（　　）

  A．6-2i

  B．4-2i

  C．6+2i

  D．4+2i
  组卷：5214引用：49难度：0.9

  解析

• 2．运动员甲10次射击成绩（单位：环）如下：7，8，9，7，4，8，9，9，7，2，则下列关于这组数据说法不正确的是（　　）

  A．众数为7和9	B．平均数为7
  C．中位数为7	D．方差为s2=4.8
  组卷：303引用：8难度：0.8

  解析

• 3．目前，甲型流感病毒在国内传播，据某市卫健委通报，该市流行的甲型流感病毒，以甲型H1N1亚型病毒为主，假如该市某小区共有100名感染者，其中有10名年轻人，60名老年人，30名儿童，现用分层抽样的方法从中随机抽取20人进行检测，则做检测的老年人人数为（　　）

  A．6

  B．10

  C．12

  D．16
  组卷：290引用：3难度：0.9

  解析

• 4．已知某圆锥的母线长为4，高为

  2

  3

  ，则圆锥的全面积为（　　）

  A．10π

  B．12π

  C．14π

  D．16π
  组卷：259引用：4难度：0.8

  解析

• 5．某校从高一新生中随机抽取了一个容量为10的身高样本，数据（单位：cm）从小到大排序下：158，165，165，167，168，169，x,172，173，175．若样本数据的第60百分位数是170，则x=（　　）

  A．169

  B．170

  C．171

  D．172
  组卷：239引用：5难度：0.8

  解析

• 6．已知向量

  a

  ，

  b

  满足

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  3

  ，

  a

  •

  b

  =

  1

  ，则

  b

  在

  a

  上的投影向量为（　　）

  A． - 1 4 a

  B． - 1 9 a

  C． 1 4 a

  D． 1 9 a
  组卷：98引用：6难度：0.7

  解析

• 7．张益唐是当代著名华人数学家．他在数论研究方面取得了巨大成就，曾经在《数学年刊》发表《质数间的有界间隔》，证明了存在无穷多对质数间隙都小于7000万.2013年张益唐证明了孪生素数猜想的一个弱化形式．孪生素数猜想是希尔伯特在1900年提出的23个问题之一，可以这样描述：存在无穷多个素数p,使得p+2是素数，素数对（p,p+2）称为孪生素数．在不超过12的素数中，随机选取两个不同的数，能够组成孪生素数的概率是（　　）

  A． 1 4

  B． 1 5

  C． 1 10

  D． 1 20
  组卷：76引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

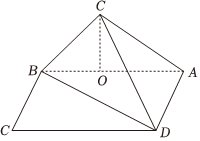• 21．如图，在矩形ABCD中，

  AB

  =

  3

  ，

  BC

  =

  1

  ，沿对角线BD把△BCD折起，使C移到C′，且C′在面ABC内的射影O恰好落在AB上．
  （1）求证：AD⊥C′B；
  （2）求AB与平面C′BD所成的角的正弦值．
  组卷：117引用：3难度：0.5

  解析

• 22．在△ABC中，内角A，B，C的对边分别为a,b,c,且

  1

  tan

  B

  +

  1

  tan

  C

  =

  1

  tan

  A

  ．
  （1）求

  b

  2

  +

  c

  2

  a

  2

  的值；
  （2）记△ABC的面积为S，点P是△ABC内一点，且∠PAB=∠PBC=∠PCA=θ，证明：
  ①

  tan

  A

  =

  4

  S

  b

  2

  +

  c

  2

  -

  a

  2

  ；
  ②tanA=2tanθ．
  组卷：46引用：2难度：0.6

  解析