2022-2023学年安徽省安庆市九一六学校高二（上）月考数学试卷（9月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知空间三点O（0，0，0），A（-1，1，0），B（0，1，1），在直线OA上有一点H满足BH⊥OA，则点H的坐标为（　　）

  A．（-2，2，0）

  B．（2，-2，0）

  C．（- 1 2 ， 1 2 ，0）

  D．（ 1 2 ，- 1 2 ，0）
  组卷：263引用：15难度：0.7

  解析

• 2．过两点A（4，y），B（2，-3）的直线的倾斜角为45°，则y=（　　）

  A．- 3 2

  B． 3 2

  C．-1

  D．1
  组卷：694引用：19难度：0.9

  解析

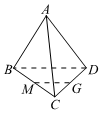• 3．如图所示空间四边形ABCD，连接AC、BD，设M、G分别是BC、CD的中点，则

  MG

  -

  AB

  +

  AD

  等于（　　）

  A． 3 2 DB

  B．3 MG

  C．3 GM

  D．2 MG
  组卷：162引用：5难度：0.9

  解析

• 4．已知过点A（-2，m）和点B（m,4）的直线与直线2x+y=1平行，则m的值为（　　）

  A．0

  B．-8

  C．2

  D．10
  组卷：23引用：1难度：0.5

  解析

• 5．在直三棱柱ABC-A₁B₁C₁中，

  AC

  =

  3

  ，

  BC

  =

  3

  ，

  AB

  =

  3

  2

  ，

  A

  A

  1

  =

  4

  ，则异面直线A₁C与BC₁所成角的余弦值为（　　）

  A． - 16 25

  B． 9 25

  C． 16 25

  D． 4 5
  组卷：284引用：15难度：0.5

  解析

• 6．直线l与直线y=1和x-y-7=0分别交于P、Q两点，线段PQ的中点坐标为（1，-1），那么直线l的斜率是（　　）

  A． 2 3

  B． - 2 3

  C． 3 2

  D． - 3 2
  组卷：296引用：8难度：0.9

  解析

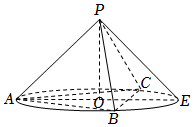• 7．如图，P为圆锥的顶点，O是圆锥底面的圆心，圆锥PO的轴截面PAE是边长为2的等边三角形，△ABC是底面圆的内接正三角形，则

  PB

  •

  PC

  =（　　）

  A． 3 2

  B． 5 2

  C． 7 2

  D． 9 2
  组卷：73引用：5难度：0.6

  解析

四、解答题：本题共6个小题，满分70分，解答应写出文字说明，证明过程或演算步骤.

• 21．如图，面积为8的平行四边形ABCD，A为坐标原点，B坐标为（2，-1），C、D均在第一象限．
  （Ⅰ）求直线CD的方程；
  （Ⅱ）若|BC|=

  13

  ，求点D的横坐标．
  组卷：289引用：9难度：0.3

  解析

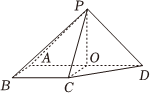• 22．如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=

  2

  ，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD的中点，问：线段AD上是否存在一点Q，使得它到平面PCD的距离为

  3

  2

  ？若存在，求出

  AQ

  QD

  的值；若不存在，请说明理由．
  组卷：27引用：5难度：0.5

  解析