2022-2023学年北京市十一学校八年级（下）第三学段诊断数学试卷

一.选择题（本题共30分，每小题3分）第1-10题均有4个选项，符合题意的选项只有1个

• 1．函数y=

  x

  +

  2

  的自变量x的取值范围是（　　）

  A．x≠-2

  B．x≥-2

  C．x＞-2

  D．x＜-2
  组卷：330引用：8难度：0.9

  解析

• 2．在平行四边形ABCD中，若∠A+∠C=100°，则∠B的度数是（　　）

  A．50°

  B．100°

  C．120°

  D．130°
  组卷：255引用：1难度：0.5

  解析

• 3．若点A（-1，y₁），B（1，y₂）都在直线y=-x+3上，则y₁与y₂的大小关系是（　　）

  A．y1＞y2	B．y1=y2
  C．y1＜y2	D．无法比较大小
  组卷：322引用：1难度：0.6

  解析

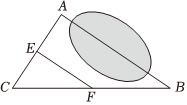• 4．如图，施工队打算测量A，B两地之间的距离，但A，B两地之间有一个池塘，于是施工队在C处取点，连接AC，BC，测量AC，BC的中点E．F之间的距离是50m,则AB两地之间距离为（　　）

  A．50m

  B．80m

  C．100m

  D．120m
  组卷：247引用：3难度：0.5

  解析

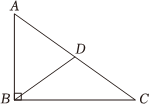• 5．如图，在△ABC中，∠ABC=90°，D为AC中点，若BD=2，则AC的长是（　　）

  A．6

  B．5

  C．4

  D．3
  组卷：604引用：5难度：0.5

  解析

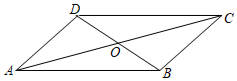• 6．如图，在四边形ABCD中，对角线AC与BD相交于点O，下列条件中不能判定四边形ABCD是平行四边形的是（　　）

  A．OA=OC，OB=OD	B．AB∥CD，AD∥CB
  C．AB=CD，AD=CB	D．AB∥CD，AD=CB
  组卷：233引用：7难度：0.5

  解析

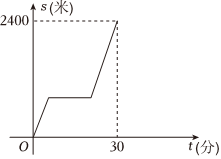• 7．某天早晨，小明从家骑自行车去上学，途中因自行车发生故障而维修了15分钟．若小明骑车的速度v始终不变，从出发开始计时，小明离家的距离x（单位：米）与时间t（单位：分钟）的对应关系如图所示，则小明骑车的速度v是（　　）

  A．120米/分

  B．150米/分

  C．160米/分

  D．200米/分
  组卷：218引用：1难度：0.7

  解析

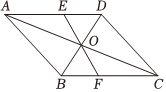• 8．如图，▱ABCD的对角线AC、BD交于点O，▱ABCD的周长为30，直线EF过点O，且与AD，BC分别交于点E．F，若OE=5，则四边形ABFE的周长是（　　）

  A．30

  B．25

  C．20

  D．15
  组卷：2198引用：10难度：0.5

  解析

三.解答题（本题共46分，第19-23题每小题5分，第24-26题每小题5分）

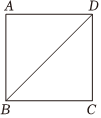• 25．如图，在正方形ABCD中，点E是对角线BD上一点（点E不与点B或点D重合），连接AE，EC．延长EC至点P使得CP=AE，连接DP．
  （1）补全图形，探究∠DCP与∠BAE满足的等量关系，并证明：
  （2）探究DP，BE．BD满足的等量关系，并证明；
  （3）AB=1，点E从点B向点D运动的过程中，直接写出△DCP面积的取值范围．
  组卷：53引用：1难度：0.1

  解析

• 26．如图1，在直角△ABC中，∠ACB=90°，若点P在斜边AB上（不与A，B重合）满足CP≤CA，则称点P是直角△ABC的“近A点”．
  在平面直角坐标系xOy中，O（0，0），一次函数图象y=kx+2与x轴，y轴分别交于点M，N．
  （1）若k=-

  3

  3

  ，点P是直角△NOM的“近N点”，则OP的长度可能是

  ；（填序号）
  ①1
  ②2
  ③

  3

  
  ④

  2

  3

  
  （2）若线段MN上的所有点（不含M和N）都是直角△NOM的“近N点”，求k的取值范围；
  （3）当|k|＞1时，若一次函数y=x+k与y=kx+2的交点恰好是直角△NOM的“近N点”．则直接写出k的取值范围是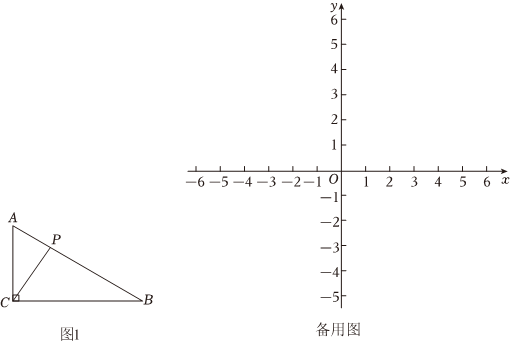

  ．
  
  组卷：428引用：3难度：0.1

  解析