2023-2024学年江西省南昌市西湖区名校联盟八年级（上）期中数学试卷

一、选择题（本大题共6小题，每小题3分，共18分）

• 1．下列图形中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：183引用：22难度：0.9

  解析

• 2．下列各组线段中，能构成三角形的是（　　）

  A．2，5，7

  B．4，4，8

  C．4，5，6

  D．4，5，10
  组卷：513引用：11难度：0.8

  解析

• 3．若一个三角形三个内角度数的比为1：2：3，那么这个三角形是（　　）

  A．锐角三角形

  B．等边三角形

  C．钝角三角形

  D．直角三角形
  组卷：561引用：25难度：0.9

  解析

• 4．到三角形各顶点距离相等的点是（　　）

  A．三条边垂直平分线交点	B．三个内角平分线交点
  C．三条中线交点	D．三条高交点
  组卷：1416引用：12难度：0.5

  解析

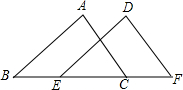• 5．如图，△ABC≌△DEF，点A与D，B与E分别是对应顶点，且测得BC=5cm,BF=7cm,则EC长为（　　）

  A．1cm

  B．2cm

  C．3cm

  D．4cm
  组卷：2444引用：59难度：0.9

  解析

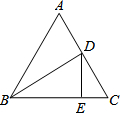• 6．如图，在等边△ABC中，BD平分∠ABC交AC于点D，过点D作DE⊥BC于点E，且CE=1.5，则AB的长为（　　）

  A．3

  B．4.5

  C．6

  D．7.5
  组卷：3045引用：33难度：0.7

  解析

二、填空题（本大题共6小题，每小题3分，共18分）

• 7．已知一个多边形的内角和为1080°，则它的边数为

  ．
  组卷：1061引用：20难度：0.8

  解析

五、解答题（本大题共2小题，每小题9分，共18分）

• 22．阅读并填空．将三角尺（△MPN，∠MPN=90°）放置在△ABC上（点P在△ABC内），如图①所示，三角尺的两边PM，PN恰好经过点B和点C．我们来探究：∠ABP与∠ACP是否存在某种数量关系．
  
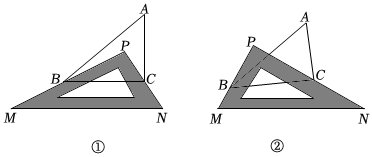
  （1）特例探索：若∠A=50°，则∠PBC+∠PCB=

  度；∠ABP+∠ACP=

  度；
  （2）类比探索：求∠ABP，∠ACP，∠A的关系，并说明理由；
  （3）变式探索：如图②所示，改变三角尺的位置，使点P在△ABC外，三角尺的两边PM，PN仍恰好经过点B和点C，求∠ABP，∠ACP，∠A的关系，并说明理由．
  组卷：1249引用：11难度：0.8

  解析

六、解答题（本大题共1小题，共12分）

• 23．通过对如图数学模型的研究学习，解决下列问题：
  [模型呈现]
  如图1，∠BAD=90°，AB=AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2=∠2+∠D=90°，得∠1=∠D．又∠ACB=∠AED=90°，可以推理得到△ABC≌△DAE．进而得到AC=

  ，BC=AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；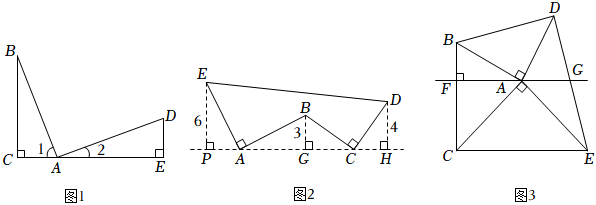
  
  [模型应用]
  如图2，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积为

  ．
  A.50
  B.62
  C.65
  D.68
  [深入探究]
  如图3，∠BAD=∠CAE=90°，AB=AD，AC=AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；
  组卷：1734引用：11难度：0.1

  解析