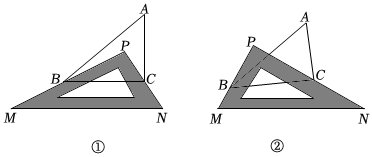
阅读并填空．将三角尺（△MPN，∠MPN=90°）放置在△ABC上（点P在△ABC内），如图①所示，三角尺的两边PM，PN恰好经过点B和点C．我们来探究：∠ABP与∠ACP是否存在某种数量关系．
（1）特例探索：若∠A=50°，则∠PBC+∠PCB=9090度；∠ABP+∠ACP=4040度；
（2）类比探索：求∠ABP，∠ACP，∠A的关系，并说明理由；
（3）变式探索：如图②所示，改变三角尺的位置，使点P在△ABC外，三角尺的两边PM，PN仍恰好经过点B和点C，求∠ABP，∠ACP，∠A的关系，并说明理由．
【考点】三角形内角和定理．
【答案】90；40
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/29 11:0:12组卷：1249引用：11难度：0.8
相似题
-
1．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：
（1）∠BAC=2；
（2）BC=2；
（3）=90°．发布：2025/1/24 8:0:2组卷：45引用：1难度：0.5 -
2．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则：
（1）∠A1=度；
（2）∠A2013=度．发布：2025/1/24 8:0:2组卷：109引用：1难度：0.5 -
3．已知：如图，△ABC中，∠ABC=∠C，BD是∠ABC的平分线，且∠BDE=∠BED，∠A=100°，求∠DEC的度数．发布：2025/1/24 8:0:2组卷：117引用：4难度：0.5
