当前位置：试卷中心 > 试卷详情

2022-2023学年山东省威海市文登区八年级（下）期末数学试卷（五四学制）

发布：2024/6/29 8:0:10

一、选择题（本大题共10小题，每小题3分，共30分

1．在实数范围内，不论x取何值，下列各式始终有意义的是（　　）
A．
2
+
x
B．
（
x
）
3
C．
x
2
+
1
D．
-
3
-
x
2
组卷：54引用：1难度：0.7
解析
2．若x：y=5：6，则下列运算不正确的是（　　）
A．
x
+
y
y
=
11
6
B．
x
-
y
y
=
1
6
C．
x
y
-
x
=
5
D．
x
+
y
y
-
x
=
11
组卷：382引用：3难度：0.7
解析
3．从对称性角度看，下列图形与其它三个图形不同的是（　　）#ZZ04
A．平行四边形 B．矩形 C．菱形 D．正方形
组卷：20引用：1难度：0.8
解析
4．下列运算正确的是（　　）
A．
2
-
2
2
=
2
B．-
1
2
2
=
-
1
2
C．
2
6
÷
1
2
3
=
2
D．（
2
+
3
）²=5
组卷：43引用：4难度：0.7
解析
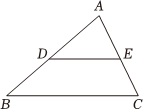5．如图，在△ABC中，点D，点E分别是AB，AC上的点，下列选项中，不能判定△ABC与△ADE相似的是（　　）
A．∠AED=∠C B．
AD
AB
=
AE
AC
C．
AD
AC
=
AE
AB
D．
AD
AB
=
DE
BC
组卷：297引用：1难度：0.7
解析
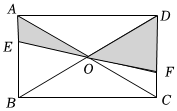6．如图，矩形ABCD，对角线AC，BD交于点O，过点O作EF分别交AB，CD于点E，点F，若AB=6，BC=8，则图中阴影部分的面积为（　　）
A．6 B．8 C．12 D．24
组卷：107引用：1难度：0.7
解析
7．某城市为了申办冬运会，决定改善城市容貌，绿化环境，计划用两年时间，使绿地面积增加44%，这两年平均每年绿地面积的增长率是（　　）
A．19% B．20% C．21% D．22%
组卷：942引用：10难度：0.6
解析
8．已知x₁，x₂是关于x的方程x²-kx-1=0的两个实数根，下列结论一定正确的是（　　）
A．x₁≠x₂ B．x₁+x₂＞0 C．x₁•x₂＞0 D．x₁＜0，x₂＜0
组卷：297引用：4难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共72分）

23．如图，Rt△ABC中，∠ACB=90°，将△ABC沿AB的方向平移得到△DEF，连接CD，FB，CF．
（1）当点D移至什么位置时，四边形CDBF是菱形，并加以证明；
（2）在（1）的条件下，四边形CDBF能否为正方形？若能，请说明理由；若不能，请给△ABC添加一个条件，使四边形CDBF为正方形，并写出推理过程．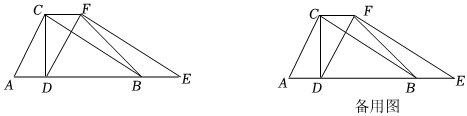
组卷：63引用：1难度：0.5
解析
24．在矩形ABCD中，AE⊥BD于点E，连接CE，过点E作EF⊥EC交AD于点F．
（1）求证：AE•AB=DE•AF；
（2）若AB=1，BC=2，求FD的长．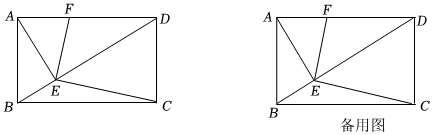
组卷：436引用：3难度：0.5
解析