2022-2023学年江苏省连云港市东海县八年级(下)期末数学试卷
发布:2024/6/21 8:0:10
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
-
1.下列新能源汽车标志图案中,既是轴对称图形又是中心对称图形的是( )
组卷:343引用:19难度:0.7 -
2.下列二次根式中,最简二次根式是( )
组卷:155引用:3难度:0.9 -
3.数轴上表示数a的点在原点左侧,表示数b的点在原点右侧,下列事件是随机事件的是( )
组卷:79引用:2难度:0.7 -
4.下表是我市5月1日-7日最高气温的记录表:
如果要更直观反映我市一周每天的最高气温的变化趋势,你认为应该采用( )5月1日 5月2日 5月3日 5月4日 5月5日 5月6日 5月7日 21℃ 25℃ 27℃ 29℃ 28℃ 30℃ 26℃ 组卷:117引用:2难度:0.7 -
5.下列点中和(-3,2)在同一个反比例函数图象上的是( )
组卷:65引用:2难度:0.5 -
6.根据分式的基本性质,分式
可变形为( )13-x组卷:391引用:3难度:0.7 -
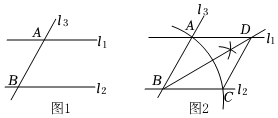 7.如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
7.如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )组卷:1260引用:6难度:0.5 -
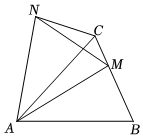 8.如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )组卷:3066引用:32难度:0.6
8.如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )组卷:3066引用:32难度:0.6
三、解答题(本题共10小题,共102分,解答时写出必要的文字说明、说理过程或演算步骤)
-
25.【问题情境】期中调研试题中的第26题对苏科版八年级下册数学教材第94页第19题第(1)题进行了探究.小明在期末复习时,对该题进行了新的探究.
【探究活动1】(1)如图,在正方形ABCD中,点E、F、G分别在边BC、CD和DA上,且GE⊥BF,垂足为M.那么GE与BF相等吗?证明你的结论;
【探究活动2】(2)如图,在(1)的条件下,当M在正方形ABCD的对角线AC上时,连接BG,将△BMG沿着BG翻折,点M落在点M'处.
①四边形BMGM′是正方形吗?请说明理由;
②若AB=6,如图,点P在AC上,且AC=3AP,直接写出M'P+M'B的最小值为 .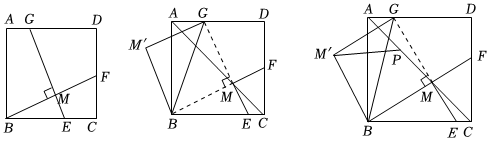 组卷:397引用:1难度:0.1
组卷:397引用:1难度:0.1 -
26.【提出定义】已知y是x的函数,当x=m时,函数值y=p;当x=n时,函数值y=q,若q=ip(i为正整数),则称m≤x≤n为该函数的i倍区间.如,函数y=-x-2中,当x=2时,y=-4,当x=10时,y=-12,-12=3×(-4),所以2≤x≤10是函数y=-x-2的3倍区间.
【理解内化】
(1)若-6≤x≤-3是函数y=的i倍区间,则i=;6x
(2)已知m≤x≤n是函数y=(k≠0)的i倍区间(i为正整数),点A(m,p)、B(n,q)是函数y=kx(k≠0)图象上的两点.kx
①试说明:n<0;
②当k=4,i=2时,求△OAB的面积;
【拓展应用】
(3)已知a≤x≤a+4是函数y=(k≠0)的3倍区间,在此区间内,该函数的最大值与最小值的差为kx,求a、k的值.52组卷:253引用:1难度:0.5


