2021-2022学年广东省佛山市南海区八年级（上）第一次学情调查数学试卷

一、选择题（本大题10小题，每小题3分，共30分）

• 1．下面各数中，无理数的是（　　）

  A．0

  B．π

  C． 22 7

  D．-|-4|
  组卷：51引用：2难度：0.8

  解析

• 2．下列运算正确的是（　　）

  A．a•a2=a3

  B．3a+2a2=5a2

  C．2-3=-8

  D． 9 =±3
  组卷：135引用：6难度：0.9

  解析

• 3．若二次根式

  x

  -

  2

  在实数范围内有意义，则x的取值范围是（　　）

  A．x＞2

  B．x≥2

  C．x＜2

  D．x≤2
  组卷：1710引用：30难度：0.8

  解析

• 4．全红婵在2021年东京奥运会女子十米跳台项目中获得了冠军，五次跳水成绩分别是（单位：分）：82.50，96.00，95.70，96.00，96.00，这组数据的众数和中位数分别是（　　）

  A．96.00，95.70	B．96.00，96.00
  C．96.00，82.50	D．95.70，96.00
  组卷：249引用：10难度：0.6

  解析

• 5．在平面直角坐标系中，点M（-3，6）关于x轴的对称点M′的坐标是（　　）

  A．（3，-6）

  B．（-3，-6）

  C．（3，6）

  D．（6，-3）
  组卷：921引用：11难度：0.9

  解析

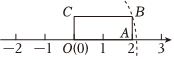• 6．如图，长方形OABC中，OA=2，AB=1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（　　）

  A． 3

  B． 2 2

  C． 5

  D．2.5
  组卷：71引用：4难度：0.5

  解析

• 7．已知点（-4，y₁），（2，y₂）都在直线

  y

  =

  -

  1

  2

  x

  -

  3

  上，则y₁，y₂的大小关系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．不能比较
  组卷：19引用：1难度：0.6

  解析

• 8．在平面直角坐标系中，将直线y=-2x向上平移3个单位，平移后的直线经过点（-1，m），则m的值为（　　）

  A．-1

  B．1

  C．-5

  D．5
  组卷：3197引用：10难度：0.7

  解析

五、解答题（三）（本大题2小题，每小题12分，共24分）

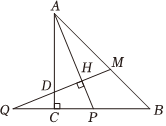• 24．在等腰直角△ABC中，AC=BC，∠ACB=90°，P是线段BC上一点（与点B、C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M．
  （1）求证：∠MQB=∠PAC；
  （2）若DQ=2，DH=

  2

  ，求HM的长；
  （3）用等式表示线段MB与CP之间的数量关系，并证明．
  组卷：17引用：2难度：0.5

  解析

• 25．在平面直角坐标系中，直线y=-

  1

  2

  x+2与x轴交于点C，与y轴交于点A．
  （1）求△AOC的周长；
  （2）点P是直线AC上的动点，过点P分别作x轴，y轴的垂线，垂足分别为点E，F，若PF=2PE，求点P的坐标；
  （3）若点B是AC中点，坐标轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？若存在，求出点M的坐标，若不存在，说明理由．
  组卷：23引用：3难度：0.3

  解析