2022-2023学年山西省晋中市八年级(上)期末数学试卷
发布:2024/8/7 8:0:9
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该选项涂黑)
-
1.
的相反数是( )2组卷:1059引用:16难度:0.9 -
 2.平面直角坐标系是法国数学家笛卡尔将代数与几何联结起来的桥梁,它使得平面图形中的点P与有序数对(x,y)建立了一一对应关系,从而能把形象的几何图形和运动过程变成代数的形式,使得用代数方法研究几何问题成为现实这种研究方法体现的数学思想是( )组卷:581引用:9难度:0.6
2.平面直角坐标系是法国数学家笛卡尔将代数与几何联结起来的桥梁,它使得平面图形中的点P与有序数对(x,y)建立了一一对应关系,从而能把形象的几何图形和运动过程变成代数的形式,使得用代数方法研究几何问题成为现实这种研究方法体现的数学思想是( )组卷:581引用:9难度:0.6 -
3.下列运算中,结果正确的是( )
组卷:150引用:1难度:0.7 -
4.下列命题中的真命题是( )
组卷:78引用:3难度:0.6 -
5.如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边AB和BC的长,再测量点A和点C间的距离,由此可推断∠B是否为直角,这样做的依据是( )
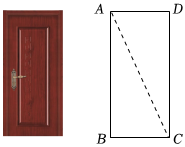 组卷:1100引用:13难度:0.5
组卷:1100引用:13难度:0.5 -
 6.中国的射击项目在世界上居于领先地位.某射击队计划从甲、乙、丙、丁四名运动员中选拔一人参加国际射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表所示:
6.中国的射击项目在世界上居于领先地位.某射击队计划从甲、乙、丙、丁四名运动员中选拔一人参加国际射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表所示:
射击队决定依据他们的平均成绩及稳定性进行选拔,那么被选中的运动员是( )甲 乙 丙 丁 /环x9.7 9.6 9.5 9.7 s2 0.035 0.042 0.036 0.015 组卷:139引用:2难度:0.7 -
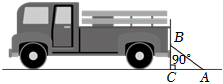 7.有一辆装货的汽车,为了方便装运货物,使用了如图所示的钢架,其中∠ACB=90°,AC=1.2m,BC=0.9m,则AB的长为( )组卷:500引用:6难度:0.6
7.有一辆装货的汽车,为了方便装运货物,使用了如图所示的钢架,其中∠ACB=90°,AC=1.2m,BC=0.9m,则AB的长为( )组卷:500引用:6难度:0.6
三、解答题(本大题共8个小题,共55分.解答应写出文字说明,证明过程或演算步骤)
-
22.请阅读下列材料,并完成相应任务.
在数学探究课上,老师出了这样一个题:如图1,锐角∠BAC内部有一点D,在其两边AB和AC上各取任意一点E,F,连接DE,DF.
求证:∠BED+∠DFC=∠BAC+∠EDF.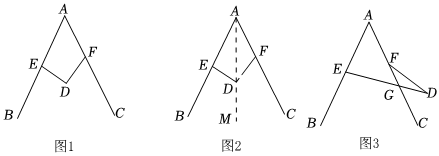
任务:小丽的证法 小红的证法 证明:
如图2,连接AD并延长至,点M,∠BED=∠BAD+∠EDA,∠DFC=∠DAC+∠ADF(依据),
又∵∠BAD+∠DAC=∠BAC,∠EDA+∠ADF=∠EDF,
∴∠BED+∠DFC=∠BAC+∠EDF.证明:
∵∠BED=80°,∠DFC=60°,∠BAC=51°,∠EDF=89°(量角器测量所得),
∴∠BED+∠DFC=140°,(计算所得).
∴∠BBED+∠DFC=∠BAC+∠EDF(等量代换).
(1)小丽证明过程中的“依据”是指数学定理:;
(2)下列说法正确的是 .
A小丽的证法用严谨的推理证明了该定理
B.小丽的证法还需要改变∠BAC的大小,再进行证明,该定理的证明才完整
C.小红的证法用特殊到一般的方法证明了该定理
D.小红的证法只要将点D在∠BAC的内部任意移动100次,重新测量进行验证,就能证明该定理
(3)如图3,若点D在锐角∠BAC外部,ED与AC相交于点G,其余条件不变,原题中结论还成立吗?若成立,请说明理由;若不成立,请探索∠BED,∠DFC,∠BAC,∠EDF之间的关系.组卷:446引用:7难度:0.8 -
23.如图,直线l1:y=
x+2和直线l2与x轴分别相交于A,B两点,且两直线相交于点C,直线l2与y轴相交于点D(0,-4),OA=2OB.12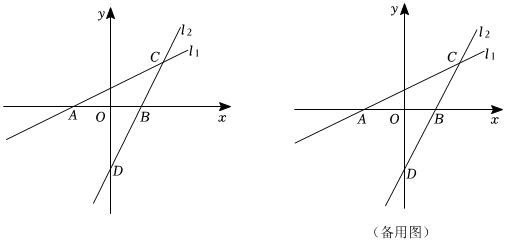
(1)求点A的坐标及直线l2的函数表达式;
(2)求△ABC的面积;
(3)试探究在x轴上是否存在点P,使得∠BDP=45°,若存在,请直接写出点P的坐标;若不存在,请说明理由.组卷:1146引用:2难度:0.3


