当前位置：试卷中心 > 试卷详情

2022-2023学年北京工业大学附中高二（上）月考数学试卷（10月份）

发布：2024/9/22 9:0:8

1．直线x+
3
y-2=0的倾斜角为（　　）
A．
π
6
B．
π
4
C．
π
3
D．
5
π
6
组卷：438引用：38难度：0.8
解析
2．若A（-1，-2），B（4，8），C（5，x），且A，B，C三点共线，则x=（　　）
A．-2 B．5 C．10 D．12
组卷：393引用：10难度：0.8
解析
3．某直线l过点B（-3，4），且在x轴上的截距是在y轴上截距的2倍，则该直线的斜率是（　　）
A．
-
4
3
B．
-
1
2
C．
4
3
或
-
1
2
D．
-
4
3
或
-
1
2
组卷：468引用：3难度：0.8
解析
4．已知直线l₁：x+y-1=0，l₂：x+m²y=0，则“m=1”是“l₁∥l₂”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：244引用：5难度：0.8
解析
5．已知点A（3，-1，0），若向量
AB
=
（
2
，
5
，-
3
）
，则点B的坐标是（　　）
A．（1，-6，3） B．（5，4，-3） C．（-1，6，-3） D．（2，5，-3）
组卷：1026引用：21难度：0.7
解析
6．若
a
=（2，3，m），
b
=（2n,6，8）且
a
，
b
为共线向量，则m+n的值为（　　）
A．7 B．
5
2
C．6 D．8
组卷：234引用：8难度：0.9
解析

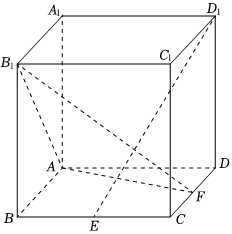18．如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点E、F分别为棱BC、CD中点．
（1）求证：D₁E⊥平面AB₁F；
（2）求直线AB与平面AB₁F所成角的正弦值．
组卷：24引用：1难度：0.5
解析
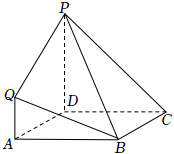19．在如图所示的几何体中，四边形ABCD是正方形，四边形ADPQ是梯形，PD∥QA，
∠
PDA
=
π
2
，平面ADPQ⊥平面ABCD，且AD=PD=2QA=2．
（1）求证：QB∥平面PDC；
（2）求平面CPB与平面PBQ所成角的大小；
（3）已知点H在棱PD上，且异面直线AH与PB所成角的余弦值为
7
3
15
，求点A到平面HBC的距离．
组卷：659引用：5难度：0.6
解析