2022-2023学年河北省唐山市曹妃甸新城实验学校（北京景山学校曹妃甸分校）高一（下）期末数学试卷

一、单选题（本大题共8小题，共40.0分.在每小题列出的选项中，选出符合题目的一项）

• 1．在复平面内，复数

  z

  =

  1

  1

  +

  3

  i

  （i为虚数单位）对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：51引用：3难度：0.8

  解析

• 2．已知

  |

  b

  |

  =

  3

  ，

  a

  在

  b

  上的投影向量为

  1

  2

  b

  ，则

  a

  •

  b

  的值为（　　）

  A．3

  B． 9 2

  C．2

  D． 1 2
  组卷：154引用：2难度：0.8

  解析

• 3．某小区约有3000人，需对小区居民身体状况进行分层抽样调查，样本中有幼龄12人，青壮龄34人，老龄14人，则该小区老龄人数的估计值为（　　）

  A．750

  B．1700

  C．600

  D．700
  组卷：94引用：3难度：0.9

  解析

• 4．设m,n是两条不同直线，α，β是两个不同平面，则下列命题中正确的是（　　）

  A．若m∥n,m∥α，n∥β，则α∥β	B．若m⊥n,m∥α，n∥β，则α∥β
  C．若m∥n,m∥α，n⊥β，则α⊥β	D．若α⊥β，m∥α，n∥β，则m∥n
  组卷：51引用：3难度：0.6

  解析

• 5．在三角形ABC中，角A，B，C对应的边分别为a,b,c,若∠A=120°，a=2，b=

  2

  3

  3

  ，则B=（　　）

  A． π 3

  B． 5 π 6

  C． π 6 或 5 π 6

  D． π 6
  组卷：150引用：8难度：0.9

  解析

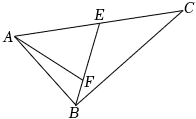• 6．如图所示，点E为△ABC的边AC的中点，F为线段BE上靠近点B的四等分点，则

  AF

  =（　　）

  A． 3 8 BA + 5 8 BC

  B． 5 4 BA + 3 4 BC

  C． - 7 8 BA + 1 8 BC

  D． - 3 4 BA + 1 4 BC
  组卷：171引用：5难度：0.7

  解析

• 7．一张储蓄卡的密码共有6位数字，每位数字都可以从0～9中任选一个，某人在银行自动提款机上取钱时，忘记了密码最后一位数字，如果任意按最后一位数字，不超过2次就按对的概率为（　　）

  A． 2 5

  B． 3 10

  C． 1 5

  D． 1 10
  组卷：90引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共70.0分.解答应写出文字说明，证明过程或演算步骤）

• 21．某社区举办环保知识有奖问答比赛，某场比赛中，甲、乙、丙三人同时回答一道问题，已知甲回答正确的概率是

  1

  2

  ，甲、丙都回答错误的概率是

  1

  8

  ，乙、丙都回答正确的概率是

  1

  2

  ．假设他们是否回答正确互不影响．
  （Ⅰ）分别求乙、丙回答正确的概率；
  （Ⅱ）求甲、乙、丙3人中不少于2人回答正确的概率．
  组卷：456引用：5难度：0.5

  解析

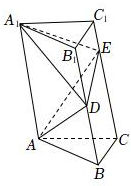• 22．如图，在直三棱柱ABC-A₁B₁C₁中，AC⊥BC，且AC=BC=

  2

  ，AA₁=2AB，D是棱BB₁的中点，E是棱CC₁上靠近C₁的四等分点．
  （Ⅰ）证明：AD⊥平面A₁DE；
  （Ⅱ）求直线AE与平面ABB₁所成角的正弦值．
  组卷：42引用：3难度：0.5

  解析