2022-2023学年江苏省泰州中学附中八年级（上）第一次月考数学试卷

一、选择题（每小题3分，共18分）

• 1．如图所示的交通标志图中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：30引用：2难度：0.9

  解析

• 2．已知等腰三角形一个内角30°，它的底角等于（　　）

  A．75°

  B．30°

  C．75°或30°

  D．不能确定
  组卷：121引用：5难度：0.9

  解析

• 3．以下列长度的线段为边，能组成直角三角形的是（其中a＞b＞c＞0）（　　）

  A．a2，b2，c2	B．a2+b2，a2-b2，2ab
  C．a+b,a-b,2ab	D．（a+b）2，（a-b）2，4ab
  组卷：15引用：1难度：0.7

  解析

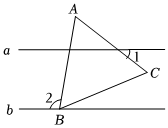• 4．如图，直线a∥b,等边△ABC的顶点B在直线b上，若∠1=35°，则∠2等于（　　）

  A．100°

  B．96°

  C．95°

  D．94°
  组卷：10引用：1难度：0.7

  解析

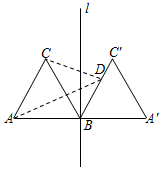• 5．如图：正△ABC的边长为3，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值（　　）

  A．6

  B．4 3

  C．3 3

  D．3+ 3
  组卷：121引用：2难度：0.7

  解析

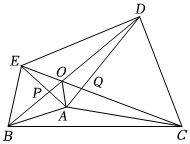• 6．如图，分别以△ABC的边AB，AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE，∠BAC=150°，AC²=3AB²，线段BD与CE相交于点O，连接BE，ED，DC，OA．有以下结论：①∠EAD=90°；②∠BOC=120°；③OA平分∠BOC；④ED=2EA；⑤BP=EQ．其中正确的结论个数是（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：409引用：2难度：0.3

  解析

二、填空题（每小题3分，共30分）

• 7．角是轴对称图形，

  是它的对称轴．
  组卷：935引用：77难度：0.7

  解析

• 8．若一个直角三角形的两边长分别为6和8，则其斜边上的中线长为

  ．
  组卷：152引用：6难度：0.6

  解析

三、解答题（共10小题，共102分）

• 25．在△ABC中，AB=AC，过点C作射线CB，使∠ACB′=∠ACB（点B′与点B在直线AC的异侧）点D是射线CB′上一动点（不与点C重合），点E在线段BC上，且∠DAE+∠ACD=90°．
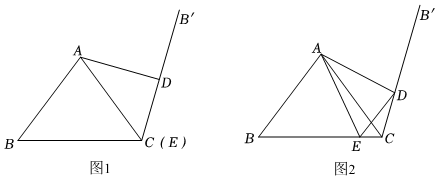
  （1）如图1，当点E与点C重合时，AD与CB′的位置关系是

  ，若BC=a,则CD的长为

  ；（用含a的式子表示）
  （2）如图2，当点E与点C不重合时，连接DE，
  ①若∠DAE=30°，求∠BAC的度数；
  ②用等式表示∠BAC与∠DAE之间的数量关系，并证明．
  组卷：69引用：1难度：0.2

  解析

• 26．在△ABD中，∠A=45°，BC⊥AD于点C，E为AB上一点，连接DE交BC于点F，且∠ADE=∠CBD．
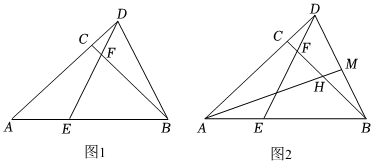
  （1）如图1，求证：DE=DB；
  （2）如图2，作AM⊥BD于点M，交BC于点H，判断并说明AH与BD的数量关系；
  （3）在（2）的条件下，当CH：BH=4：7时，
  ①若△ADE的面积为30，求线段AD的值；
  ②求

  AM

  BD

  ．
  组卷：36引用：1难度：0.3

  解析