2023-2024学年吉林省白城市通榆九中、育才学校八年级(上)第一次月考数学试卷(9月份)
发布:2024/8/26 20:0:9
一、单项选择题(每小题2分,共12分)
-
1.下面分别是三根小木棒的长度,能摆成三角形的是( )
组卷:821引用:20难度:0.8 -
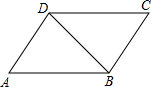 2.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )组卷:2958引用:52难度:0.9
2.如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )组卷:2958引用:52难度:0.9 -
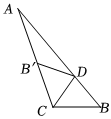 3.如图,在△ABC中,∠ACB=110°,∠A=20°,D是AB上一点,将△ABC沿CD折叠,使点B落在AC边上的点B'处,则∠ADB'等于( )组卷:23引用:3难度:0.7
3.如图,在△ABC中,∠ACB=110°,∠A=20°,D是AB上一点,将△ABC沿CD折叠,使点B落在AC边上的点B'处,则∠ADB'等于( )组卷:23引用:3难度:0.7 -
 4.如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )组卷:761引用:36难度:0.7
4.如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )组卷:761引用:36难度:0.7 -
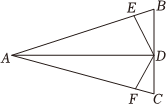
 5.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为( )组卷:2087引用:16难度:0.9
5.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为( )组卷:2087引用:16难度:0.9 -
 6.如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )
6.如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )
①AD平分∠EDF;②△EBD≌△FCD;③BD=CD;④AD⊥BC.组卷:190引用:8难度:0.7
二、填空题(每小题3分,共24分)
-
7.三角形三个内角的度数比为3:4:5,其最大外角的度数为 °.
组卷:54引用:1难度:0.7 -
8.△ABC≌△DEF,且△ABC的周长为15,若AB=6,EF=5,AC=
.组卷:57引用:2难度:0.9
六、解答题(每小题10分,共20分)
-
25.如图,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC于点E,点F在AE上且CF∥AD.
(1)如图①,若△ABC是锐角三角形,∠B=30°,∠ACB=80°,则∠CFE=度.
(2)如图①,若△ABC是锐角三角形,∠ACB>∠B,∠B=x,∠ACB=y,则∠CFE=(用含x,y的代数式表示).
(3)如图②,若△ABC是钝角三角形,∠ACB为钝角,其余条件不变,则(2)中的结论还成立吗?说明理由.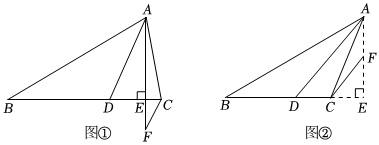 组卷:72引用:1难度:0.7
组卷:72引用:1难度:0.7 -
26.如图①,∠ACB=90°,AC=BC,过点C的直线l不经过△ABC的内部,过点A,B分别作l的垂线,垂足为D,E.

(1)请你在图①中,找出一对全等三角形:.
(2)请证明你的结论.
(3)尝试探究:若AD=a,BE=b.
图①中四边形ADEB的面积为 (用含a,b的代数式表示).
如图②,若过点C的直线l经过△ABC的内部,其余条件不变,则四边形ADBE的面积为 (用含a,b的代数式表示).
(4)拓展应用:如图③,若A(-2,0),C(0,4),则点B的坐标为 .若点P(不与点B重合)在坐标平面内,△ABC与△ACP全等,则点P的坐标为 .组卷:31引用:1难度:0.4


