微专题探究学习：阅读探究学习过程，完成（1）小题中的填空、（2）小题的图形设计和（3）小题的求面积．
《面积与完全平方公式》
如图1，阴影部分是一个边长为a的大正方形剪去一个边长为b的小正方形和两个宽为b的长方形之后所剩余的部分．
（1）①图1中剪去的长方形的长为 a-ba-b，面积为 ab-b2ab-b2．
②用两种方式表示阴影部分的面积为 （a-b）2（a-b）2或 a2-2ab+b2a2-2ab+b2，由此可以验证的公式为 （a-b）2=a2-2ab+b2（a-b）2=a2-2ab+b2．
（2）请设计一个新的图形验证公式：（a+b）2=a2+2ab+b2
（3）如图2，S1，S2分别表示边长为a,b的正方形的面积，且A，B，C三点在一条直线上，若S1+S2=40，AB=8，求图中阴影部分的面积．
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】a-b；ab-b2；（a-b）2；a2-2ab+b2；（a-b）2=a2-2ab+b2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：728引用：3难度：0.5
相似题
-
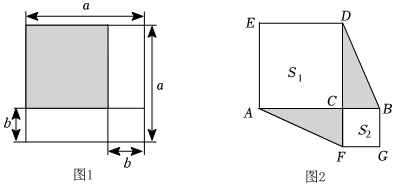
1．学习整式乘法时，老师拿出三种型号卡片，如图1．
（1）利用多项式与多项式相乘的法则，计算：（a+2b）（a+b）=；
（2）选取1张A型卡片，4张C型卡片，则应取 张B型卡片才能用它们拼成一个新的正方形，此新的正方形的边长是 （用含a,b的代数式表示）；
（3）选取4张C型卡片在纸上按图2的方式拼图，并剪出中间正方形作为第四种D型卡片，由此可检验的等量关系为 ；
（4）选取1张D型卡片，3张C型卡片按图3的方式不重复的叠放长方形MNPQ框架内，已知NP的长度固定不变，MN的长度可以变化，且MN≠0．图中两阴影部分（长方形）的面积分别表示为S1，S2，若S1-S2=3b2，则a与b有什么关系？请说明理由．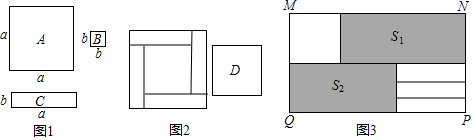
发布：2024/12/23 18:0:1组卷：3664引用：6难度：0.1 -
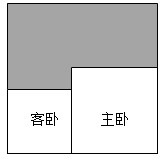2．如图所示的是正方形的房屋结构平面图，其中主卧与客卧都是正方形，其面积之和比其余面积（阴影部分）多6.25m2，则主卧与客卧的周长差是（ ）发布：2025/1/1 6:30:3组卷：207引用：4难度：0.6 -
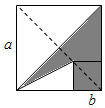3．如图，两个正方形边长分别为a,b,如果a+b=10，ab=18，则阴影部分的面积为．发布：2024/12/23 18:0:1组卷：2015引用：6难度：0.5
