2023-2024学年江苏省南通市海安高级中学高二（上）段考数学试卷（一）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x|x²-2x＜0}，集合

  B

  =

  {

  y

  |

  y

  =

  lo

  g

  2

  （

  2

  -

  x

  2

  ）

  }

  ，则A∪B=（　　）

  A．（0，1]

  B．（-∞，1）

  C．（-∞，2）

  D．（0，2）
  组卷：42引用：2难度：0.7

  解析

• 2．已知复数z满足zi+3=2i,则

  |

  z

  -

  i

  |

  =（　　）

  A． 2 2

  B． 3 2

  C． 2 5

  D． 5
  组卷：42引用：4难度：0.7

  解析

• 3．“m＜1”是“点P（1，1）在圆C：x²+y²-2mx=0外”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分又不必要条件
  组卷：48引用：4难度：0.7

  解析

• 4．已知函数f（x）与g（x）的部分图象如图1，则图2可能是下列哪个函数的部分图象（　　）
  

  A．y=f（g（x））

  B．y=f（x）g（x）

  C．y=g（f（x））

  D．y= f （ x ） g （ x ）
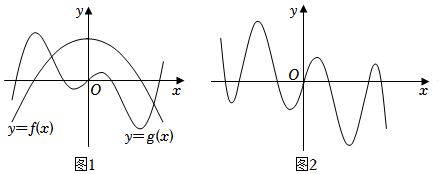  组卷：137引用：6难度：0.7

  解析

• 5．若动点A（x₁，y₁），B（x₂，y₂）分别在直线l₁：x+y-7=0和l₂：x+y-5=0上移动，则AB中点M到原点距离的最小值为（　　）

  A．3 2

  B．2 3

  C．3 3

  D．4 2
  组卷：979引用：15难度：0.5

  解析

• 6．已知圆C：x²+y²=4，从点E（-4，0）出发的光线要想不被圆C挡住直接到达点F（3，m），则实数m的取值范围为（　　）

  A． （ - 7 3 3 ， 7 3 3 ）	B． （ - ∞ ，- 7 3 3 ） ∪ （ 7 3 3 ， + ∞ ）
  C． （ - 3 3 ， 3 3 ）	D． （ - ∞ ，- 3 3 ） ∪ （ 3 3 ， + ∞ ）
  组卷：173引用：4难度：0.7

  解析

• 7．设函数f（x）=2sin（ωx+φ）-1（ω＞0），若对于任意实数φ，f（x）在区间[

  π

  4

  ，

  3

  π

  4

  ]上至少有2个零点，至多有3个零点，则ω的取值范围是（　　）

  A．[ 8 3 ， 16 3 ）

  B．[4， 16 3 ）

  C．[4， 20 3 ）

  D．[ 8 3 ， 20 3 ）
  组卷：3592引用：18难度：0.2

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知圆M与直线x=2相切，圆心M在直线x+y=0上，且直线x-y-2=0被圆M截得的弦长为

  2

  2

  ．
  （1）求圆M的方程；
  （2）若在x轴上的截距为-1且不与坐标轴垂直的直线l与圆M交于A，B两点，在x轴上是否存在定点Q，使得k_AQ+k_BQ=0？若存在，求出Q点坐标；若不存在，说明理由．
  组卷：247引用：2难度：0.5

  解析

• 22．如图所示，四棱锥P-ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2．
  （1）证明：平面PBE⊥平面PAB；
  （2）求点D到平面PBE的距离；
  （3）求平面PAD和平面PBE所成锐二面角的余弦值．
  组卷：328引用：4难度：0.5

  解析