2021-2022学年福建省三明市宁化县七年级（下）期中数学试卷

一、选择题（本大题共10小题，共40分）

• 1．下列运算正确的是（　　）

  A．a2+a2=a4

  B．a3•a4=a12

  C．（a3）4=a12

  D．（ab）2=ab2
  组卷：266引用：5难度：0.8

  解析

• 2．我们知道，圆的周长公式是：C=2πr,那么在这个公式中，以下关于变量和常量的说法正确的是（　　）

  A．2π是常量，C，r是变量	B．2是常量，C，π，r是变量
  C．2是常量，r是变量	D．2是常量，C，r是变量
  组卷：60引用：4难度：0.7

  解析

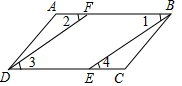• 3．如图，点F，E分别在线段AB和CD上，下列条件能判定AB∥CD的是（　　）

  A．∠1=∠2

  B．∠1=∠4

  C．∠4=∠2

  D．∠3=∠4
  组卷：1336引用：23难度：0.9

  解析

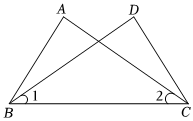• 4．如图，已知∠ABC=∠DCB，添加下列条件，不能使△ABC≌△DCB的是（　　）

  A．AC=DB

  B．AB=DC

  C．∠A=∠D

  D．∠1=∠2
  组卷：643引用：11难度：0.7

  解析

• 5．下列各式中，不能用平方差公式计算的是（　　）

  A．（x-2y）（2y+x）	B．（x-2y）（-x-2y）
  C．（x+2y）（-x-2y）	D．（2y-x）（-x-2y）
  组卷：182引用：3难度：0.8

  解析

• 6．若∠α与∠β是内错角，且∠α=50°，则∠β的度数为（　　）

  A．50°

  B．130°

  C．50°或130°

  D．无法确定
  组卷：422引用：15难度：0.9

  解析

• 7．在某次实验中，测得两个变量m和v之间的4组对应数据如下表

  m	1	2	3	4
  v	2.01	4.9	10.03	17.1

  则m与v之间的关系最接近于下列各关系式中的（　　）

  A．v=2m

  B．v=m2+1

  C．v=3m-1

  D．v=3m+1
  组卷：937引用：9难度：0.9

  解析

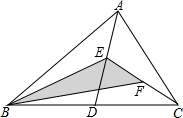• 8．如图，在△ABC中，已知点D，E，F分别是BC，AD，CE的中点，且△ABC的面积为16，则△BEF的面积是（　　）

  A．2

  B．4

  C．6

  D．8
  组卷：4390引用：21难度：0.5

  解析

三、解答题（本大题共9小题，共86分）

• 24．阅读以下材料：
  对数的创始人是苏格兰数学家纳皮尔（J．Napier,1550∼1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Euler,1707∼1783年）才发现指数与对数之间的联系．
  对数的定义：一般地，若a^x=N（a＞0，a≠1），则x叫做以a为底N的对数，记作x=log_aN．如指数式2⁴=16可以转化为4=log₂16，对数式2=log₅25可以转化为5²=25．我们根据对数的定义可得到对数的一个性质：
  log_a（M•N）=log_aM+log_aN（a＞0，a≠1，M＞0，N＞0）．
  理由如下：设log_aM=m,log_aN=n,则M=a^m，N=aⁿ．
  ∴M•N=a^m•aⁿ=a^m+n．
  由对数的定义，得m+n=log_a（M•N）．
  又∵m+n=log_aM+log_aN，
  ∴log_a（M•N）=log_aM+log_aN．
  解答下列问题：
  （1）将指数式3⁴=81转化为对数式：

  ；
  （2）求证：

  log

  a

  M

  N

  =

  log

  a

  M

  -

  log

  a

  N

  （

  a

  ＞

  0

  ，

  a

  ≠

  1

  ，

  M

  ＞

  0

  ，

  N

  ＞

  0

  ）

  ；
  （3）拓展运用：计算：log₈32+log₈4-log₈2．
  组卷：131引用：1难度：0.5

  解析

• 25．（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，BD⊥直线l,CE⊥直线l,垂足分别为点D、E．证明：DE=BD+CE．
  （2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线l上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
  （3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点．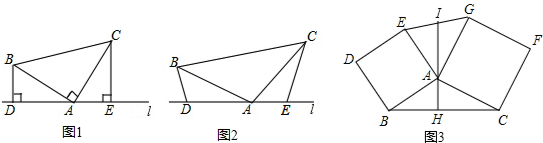
  
  组卷：13393引用：41难度：0.3

  解析