2022-2023学年辽宁省葫芦岛市兴城高级中学等四校高二（上）月考数学试卷（12月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知向量

  a

  =（2x,1，3），

  b

  =（1，-2y,9），若

  a

  ∥

  b

  ，则（　　）

  A．x=1，y=1

  B．x= 1 2 ，y=- 1 2

  C．x= 1 6 ，y=- 3 2

  D．x=- 1 6 ，y= 3 2
  组卷：383引用：40难度：0.9

  解析

• 2．已知

  C

  x

  34

  =

  C

  3

  x

  -

  6

  34

  ，则x=（　　）

  A．3或10

  B．3

  C．17

  D．3或17
  组卷：36引用：3难度：0.9

  解析

• 3．抛物线y=4x²的焦点坐标是（　　）

  A．（0， 1 8 ）

  B．（0， 1 16 ）

  C．（0， 1 4 ）

  D．（0， 1 2 ）
  组卷：86引用：4难度：0.7

  解析

• 4．公元五世纪，数学家祖冲之估计圆周率π的范围是：3.1415926＜π＜3.1415927，为纪念祖冲之在圆周率方面的成就，把3.1415926称为“祖率”，这是中国数学的伟大成就．小明是个数学迷，他在设置手机的数字密码时，打算将圆周率的前6位数字3，1，4，1，5，9进行某种排列得到密码．如果排列时要求两个1不相邻，那么小明可以设置的不同密码有（　　）个

  A．240

  B．360

  C．600

  D．720
  组卷：310引用：11难度：0.8

  解析

• 5．若直线l₁：x+my+1=0与l：2x-y=0垂直，直线l₂的方程为2x+2my+3=0，则l₁与l₂间的距离为（　　）

  A． 2 5 5

  B． 4 5 5

  C． 5 10

  D． 5 5
  组卷：88引用：2难度：0.7

  解析

• 6．与双曲线

  x

  2

  4

  -

  y

  2

  8

  =1有共同渐近线，且经过点（2，4）的双曲线的虚轴的长为（　　）

  A．2 2

  B．4 2

  C．2

  D．4
  组卷：21引用：1难度：0.8

  解析

• 7．已知Rt△EFG的直角顶点E在平面α内，斜边FG∥α，且FG=12，EF，EG与平面α分别成30°和45°角，则FG到平面α的距离是（　　）

  A． 5

  B． 6

  C． 2 3

  D． 2 6
  组卷：16引用：3难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.

• 21．设点P为圆C：x²+y²=4上的动点，过点P作x轴垂线，垂足为点Q，动点M满足

  2

  MQ

  =

  3

  PQ

  （点P、Q不重合）
  （1）求动点M的轨迹方程E；
  （2）若过点T（4，0）的动直线与轨迹E交于A、B两点，定点N为

  （

  1

  ，

  3

  2

  ）

  ，直线NA的斜率为k₁，直线NB的斜率为k₂，试判断k₁+k₂是否为定值．若是，求出该定值；若不是，请说明理由．
  组卷：94引用：4难度：0.4

  解析

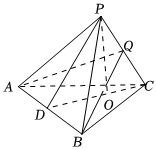• 22．如图，三棱锥P-ABC中，点P在底面的射影O在△ABC的高CD上，Q是侧棱PC上一点，截面QAB与底面ABC所成的二面角的大小等于∠OPC的大小．
  （1）求证：PC⊥平面QAB；
  （2）若DQ=4，PC=DC，PQ=DA=DB=2，求平面ABP与平面BPC所成夹角的余弦值．
  组卷：70引用：6难度：0.5

  解析