2023-2024学年重庆市万州二中高三（上）月考数学试卷（7月份）

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合P={x∈N|0≤x≤3}，Q={x|x²-1＞0}，则P∩Q=（　　）

  A．[1，3]

  B．（1，3]

  C．{2，3}

  D．{1，2，3}
  组卷：414引用：4难度：0.9

  解析

• 2．函数

  y

  =

  cosx

  •

  （

  e

  x

  -

  1

  e

  x

  +

  1

  ）

  的图象大致为（　　）

  A．	B．
  C．	D．
  组卷：9引用：1难度：0.7

  解析

• 3．已知圆台O₁O的上、下底面半径分别为r,R，高为h,平面α经过圆台O₁O的两条母线，设α截此圆台所得的截面面积为S，则（　　）

  A．当h≥R-r时，S的最大值为（R+2r）h

  B．当h≥R-r时，S的最大值为 （ R + r ） [ h 2 + （ R - r ） 2 ] 2 （ R - r ）

  C．当h＜R-r时，S的最大值为（R+2r）h

  D．当h＜R-r时，S的最大值为 （ R + r ） [ h 2 + （ R - r ） 2 ] 2 （ R - r ）
  组卷：199引用：5难度：0.5

  解析

• 4．已知抛物线C：y²=2px（p＞0）的焦点为F，准线为l,过点F作斜率为

  4

  2

  7

  的直线与C在第一象限内相交于点P，过点P作PM⊥l于点M，连接MF交C于点N，若

  MF

  =

  λ

  NF

  ，则λ的值为（　　）

  A．2

  B．3

  C．4

  D．6
  组卷：148引用：4难度：0.5

  解析

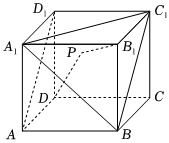• 5．如图，在棱长为3的正方体ABCD-A₁B₁C₁D₁中，点P是平面A₁BC₁内一动点，且满足|PD|+|PB₁|=2+

  13

  ，则直线B₁P与直线AD₁所成角的余弦值的取值范围为（　　）

  A．[0， 1 2 ]

  B．[0， 1 3 ]

  C．[ 1 2 ， 2 2 ]

  D．[ 1 2 ， 3 2 ]
  组卷：941引用：5难度：0.5

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  π

  4

  ）

  （ω＞0）在区间[0，π]上有且仅有4条对称轴，给出下列四个结论：
  ①f（x）在区间（0，π）上有且仅有3个不同的零点；
  ②f（x）的最小正周期可能是

  π

  2

  ；
  ③ω的取值范围是

  [

  13

  4

  ，

  17

  4

  ）

  ；
  ④f（x）在区间

  （

  0

  ，

  π

  15

  ）

  上单调递增．
  其中所有正确结论的序号是（　　）

  A．①④

  B．②③

  C．②④

  D．②③④
  组卷：2564引用：14难度：0.3

  解析

• 7．点A（x₀，y₀）（x₀＞1，y₀＜0），B，C均在抛物线y²=4x上，若直线AB，AC分别经过两定点（-1，0），M（1，4），则BC经过定点N．直线BC，MN分别交x轴于D，E，O为原点，记|OD|=a,|DE|=b,则

  a

  2

  a

  +

  1

  +

  b

  2

  b

  +

  3

  的最小值为（　　）

  A． 1 2

  B． 1 4

  C． 1 3

  D． 1 5
  组卷：447引用：3难度：0.2

  解析

四、解答题：本题共6小题，共70分。

• 21．已知椭圆C的两个顶点分别为A（-2，0），B（2，0），焦点在x轴上，离心率为

  3

  2

  ．
  （1）求椭圆C的方程；
  （2）若直线y=k（x-1）（k≠0）与x轴交于点P，与椭圆C交于M，N两点，线段MN的垂直平分线与x轴交于Q，求

  MN

  PQ

  的取值范围．
  组卷：362引用：4难度：0.5

  解析

• 22．已知函数f（x）=

  ax

  e

  x

  的图象在x=0处的切线方程为y=x,其中e是自然对数的底数．
  （1）若对任意的x∈（0，2），都有f（x）＜

  1

  k

  +

  2

  x

  -

  x

  2

  成立，求实数k的取值范围；
  （2）若函数g（x）=lnf（x）-b（b∈R）的两个零点为x₁，x₂（x₁＜x₂），试判断

  g

  ′

  （

  x

  1

  +

  x

  2

  2

  ）

  的正负，并说明理由．
  组卷：66引用：2难度：0.1

  解析