2022-2023学年福建省厦门外国语学校七年级（下）期末数学试卷

一、选择题（本大题共10小题.每小题4分，共40分，每小题只有一个选项符合题意）

• 1．下列长度的三条线段，能组成三角形的是（　　）

  A．3，4，5

  B．3，4，9

  C．5，6，11

  D．12，4，6
  组卷：97引用：1难度：0.5

  解析

• 2．已知点P（-1，4），则以下判断正确的是（　　）

  A．点P在第一象限	B．点P在第三象限
  C．点P在第四象限	D．点P到x轴的距离为4
  组卷：81引用：1难度：0.8

  解析

• 3．已知x＞y,下列不等式一定成立的是（　　）

  A．3x＜3y

  B．x+3＞y+3

  C．-2x＞-2y

  D．x-y＜0
  组卷：66引用：1难度：0.8

  解析

• 4．将不等式组

  x + 1 ＞ 2

  3 x - 2 ≤ 7

  的解集在数轴上表示出来，应是（　　）

  A．	B．
  C．	D．
  组卷：193引用：2难度：0.7

  解析

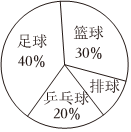• 5．某学校开展课后服务，其中在体育类活动中开设了四种运动项目：乒乓球、排球、篮球、足球，为了解学生最喜欢哪一种运动项目，随机选取100名学生进行问卷调查（每位学生仅选一种），并将调查结果绘制成如图所示的扇形统计图．下列说法错误的是（　　）

  A．“排球”对应扇形的圆心角为10°

  B．最喜欢篮球的人数占被调查人数的30%

  C．这100名学生中最喜欢足球的有40人

  D．本次调查的样本容量为100
  组卷：99引用：1难度：0.7

  解析

• 6．一元一次不等式

  x

  -

  x

  -

  1

  2

  ≥

  x

  +

  2

  3

  去分母，正确的是（　　）

  A．6x-3（x-1）≥2（x+2）	B．6x-3（x-1）≥x+2
  C．x-3（x-1）≥2（x+2）	D．x-（x-1）≥2（x+2）
  组卷：117引用：1难度：0.8

  解析

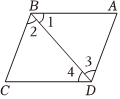• 7．如图，下列推理中正确的是（　　）

  A．∵∠1=∠4，∴BC∥AD

  B．∵∠BCD+∠ADC=180°，∴BC∥AD

  C．∵∠2=∠3，∴AB∥BC

  D．∵∠CBA+∠C=180°，∴BC∥AD
  组卷：148引用：2难度：0.6

  解析

• 8．已知

  x = 1

  y = 1

  是关于x,y的二元一次方程组

  mx + ny = - 1

  mx - 2 ny = 2

  的解，则2m-n的值为（　　）

  A．-2

  B．2

  C．-1

  D．1
  组卷：141引用：1难度：0.8

  解析

三、解答题（本大题共9题，共86分）

• 24．阅读下列材料：
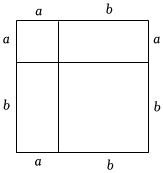
  正方形的边长为a,则其面积为a²．若正方形的边长增加b,则其面积是多少？
  探究：如图把正方形分割成四个正方形或长方形，从中可以求得正方形面积是（a+b）²，同时又可以求得正方形的面积是（a+b）²=a²+ab+ab+b²=a²+2ab+b²．
  所以可以得到：（a+b）²=a²+2ab+b²．
  我们把公式（a+b）²=a²+2ab+b²称为完全平方公式．
  例如：13²=（10+3）²=10²+2×10×3+3²=169．
  （1）探究1：请模仿上述例子进行填空：32²=（30+2）²=

  =

  ．
  （2）探究2：

  2

  究竟有多大呢？探究并完成填空：
  我们知道面积是2的正方形的边长是

  2

  ，并且

  2

  ＞1.4．设

  2

  =1.4+x,则2=（1.4+x）²，由完全平方公式可得：2=（1.4+x）²=

  ．
  ∵x的值很小，∴x²的值更小，可以略去，得：2≈2.8x+1.96
  解得：x=

  .（保留到0.001）∴

  2

  =1.4+x≈

  ．
  （3）探究3：

  2

  是不是有理数呢？
  假设

  2

  是有理数，那么存在两个互质的正整数m,n,使得

  2

  =

  n

  m

  ，
  于是有2m²=n²
  ∵2m²是偶数，∴n²也是偶数，∴n是偶数．
  设n=2t（t是正整数），则n²=4t²即4t²=2m²，
  ∴2t²=m²，∴m也是偶数．
  ∴m,n都是偶数，不互质，与假设矛盾．∴假设错误．
  ∴

  2

  不是有理数．
  解决问题：请你探究

  3

  6

  是不是有理数．
  组卷：267引用：1难度：0.5

  解析

• 25．热爱数学的小厦同学在平面直角坐标系中选取了直线l上的两点A（-4，0）和B（0，2），然后如图1所示摆放一个直尺，使直尺边缘恰好经过这两个点，他惊奇地发现直线l上的任意一点沿直线l移动时，其坐标变化是有规律的．
  （1）【描述规律】我们发现：①将点A沿此直线移动到点B时，横坐标增加了4个单位长度，纵坐标增加了

  个单位长度；将点B沿此直线移动到点（2，3）时，横坐标增加了2个单位长度，其纵坐标增加了

  个单位长度；
  ②现将直线l上任意一点P（m,n）沿直线l平移至点Q，若点Q的横坐标为m+t,则点Q的纵坐标为

  （用含n、t的式子表示）；
  （2）【应用规律】如图1，继续在直尺边缘放置一个三角形纸板ADC，点C（-6，a），点D（-3，-3），将三角形纸板ADC紧靠直尺边缘向上推动至△EFG的位置，其中点A的对应点是点E（a+t,q），点D的对应点是点F（2t+5a,n），点C的对应点是点G，求点G的坐标；（可直接使用（1）中的规律）
  （3）在（2）的条件下，如图2所示，点H（s,0）在x轴上，其中0＜s＜1，点K在直线DF上，∠BHK=130°，在∠EBH内部有一点N，使∠HBN=3∠EBN，∠BNK=80°，若四边形BHKN为凸四边形，则请在图2中画出示意图，并求∠HKN与∠NKF的数量关系．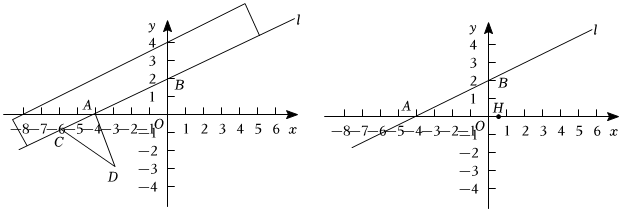
  
  组卷：189引用：1难度：0.3

  解析