阅读下列材料：
正方形的边长为a,则其面积为a²．若正方形的边长增加b,则其面积是多少？
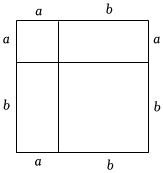
探究：如图把正方形分割成四个正方形或长方形，从中可以求得正方形面积是（a+b）²，同时又可以求得正方形的面积是（a+b）²=a²+ab+ab+b²=a²+2ab+b²．
所以可以得到：（a+b）²=a²+2ab+b²．
我们把公式（a+b）²=a²+2ab+b²称为完全平方公式．
例如：13²=（10+3）²=10²+2×10×3+3²=169．
（1）探究1：请模仿上述例子进行填空：32²=（30+2）²=

30²+2×30×2+2²

30²+2×30×2+2²

=

1024

1024

．
（2）探究2：

2

究竟有多大呢？探究并完成填空：
我们知道面积是2的正方形的边长是

2

，并且

2

＞1.4．设

2

=1.4+x,则2=（1.4+x）²，由完全平方公式可得：2=（1.4+x）²=

1.96+2.8x+x²

1.96+2.8x+x²

．
∵x的值很小，∴x²的值更小，可以略去，得：2≈2.8x+1.96
解得：x=

0.014

0.014

.（保留到0.001）∴

2

=1.4+x≈

1.414

1.414

．
（3）探究3：

2

是不是有理数呢？
假设

2

是有理数，那么存在两个互质的正整数m,n,使得

2

=

n

m

，
于是有2m²=n²
∵2m²是偶数，∴n²也是偶数，∴n是偶数．
设n=2t（t是正整数），则n²=4t²即4t²=2m²，
∴2t²=m²，∴m也是偶数．
∴m,n都是偶数，不互质，与假设矛盾．∴假设错误．
∴

2

不是有理数．
解决问题：请你探究

3

6

是不是有理数．