2023年重庆市南开中学高考数学第三次质检试卷

一、单项选择题：本题共8小题．每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．

• 1．已知复数

  z

  =

  3

  i

  1

  -

  i

  （i为虚数单位），则z的虚部为（　　）

  A．-3

  B． 3 2 i

  C． - 3 2

  D． 3 2
  组卷：18引用：3难度：0.8

  解析

• 2．已知

  e

  1

  ，

  e

  2

  是不共线的向量，则λ=-2是向量

  a

  =

  2

  e

  1

  +

  λ

  e

  2

  ，

  b

  =

  （

  λ

  +

  1

  ）

  e

  1

  +

  e

  2

  平行的（　　）条件．

  A．必要不充分	B．充分不必要
  C．充分必要	D．既不充分也不必要
  组卷：20引用：3难度：0.8

  解析

• 3．某国有企业响应国家关于进一步深化改革，加强内循环的号召，不断自主创新提升产业技术水平，同时积极调整企业旗下的甲、乙、丙、丁、戊等5种系列产品的结构比例，近年来取得了显著效果．据悉该企业2021年5种系列产品年总收入是2020年的2倍，其中5种系列产品的年收入构成比例如图所示．则以下说法错误的是（　　）
  

  A．2021年甲系列产品收入和2020年的一样多

  B．2021年乙和丙系列产品收入之和比2020年的企业年总收入还多

  C．2021年丁系列产品收入是2020年丁系列产品收入的 1 3

  D．2021年戊系列产品收入是2020年戊系列产品收入的2倍还多
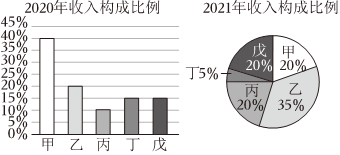  组卷：87引用：8难度：0.7

  解析

• 4．已知平面向量

  a

  ，

  b

  ，

  c

  满足：

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  3

  ，

  a

  ⊥

  （

  a

  -

  b

  ）

  且

  2

  a

  -

  b

  +

  c

  =

  0

  ，则

  |

  c

  |

  为（　　）

  A．1

  B．3

  C． 3

  D．9
  组卷：76引用：4难度：0.6

  解析

• 5．已知A，B是函数

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  -

  π

  4

  ）

  （

  ω

  ＞

  0

  ，

  x

  ∈

  R

  ）

  的图像上的两个相邻最高点和最低点，且

  |

  AB

  |

  =

  2

  2

  ，为得到g（x）=cosωx的图像，只需要将函数f（x）的图像（　　）

  A．向左平移 3 2 个单位长度

  B．向右平移π个单位长度

  C．向左平移 3 2 π 个单位长度

  D．向右平移3个单位长度
  组卷：59引用：3难度：0.7

  解析

• 6．已知实数a,b,c满足3×4^a-4^b+1=0，

  3

  b

  +

  1

  =

  3

  c

  ，

  a

  =

  c

  +

  lo

  g

  5

  （

  x

  2

  -

  x

  +

  3

  ）

  （

  x

  ∈

  R

  ）

  ，则a,b,c的大小关系是（　　）

  A．a＞b＞c

  B．b＞c＞a

  C．c＞b＞a

  D．a＞c＞b
  组卷：45引用：3难度：0.8

  解析

• 7．若f（x）=ax-lnx在[1，3]上存在x₁＜x₂满足，x₂-x₁≥1且f（x₁）=f（x₂），则实数a的取值范围是（　　）

  A． [ ln 3 2 ， 1 2 ln 3 ]

  B． [ 1 2 ln 3 ， ln 2 ]

  C． [ ln 3 2 ， ln 2 ]

  D．（0，ln2]
  组卷：50引用：2难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  3

  2

  ，椭圆的上顶点B到两焦点的距离之和为4．
  （1）求椭圆C的标准方程；
  （2）若直线l：y=kx+m与椭圆C交于异于点B的两点P，Q，直线BP，BQ与x轴相交于M（x_M，0），N（x_N，0），若

  1

  x

  M

  +

  1

  x

  N

  =1，求证：直线l过一定点，并求出定点坐标．
  组卷：453引用：5难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  lnx

  +

  3

  m

  x

  ．
  （1）若函数f（x）与x轴相切，求m的值；
  （2）若函数f（x）恰好有两个零点x₁，x₂（0＜x₂＜x₁），证明：

  1

  x

  1

  +

  3

  x

  2

  ≥

  1

  m

  ．
  组卷：96引用：3难度：0.5

  解析