2022-2023学年安徽省芜湖市无为三中八年级（下）期中数学试卷

一、选择题（每题4分，共40分）

• 1．下列二次根式中，是最简二次根式的是（　　）

  A． 1 2

  B． 15

  C． 12

  D． 25 a
  组卷：240引用：7难度：0.8

  解析

• 2．已知

  a

  +

  1

  a

  =

  7

  ，则

  a

  -

  1

  a

  =（　　）

  A． 3

  B．- 3

  C． ± 3

  D． ± 11
  组卷：3563引用：36难度：0.9

  解析

• 3．已知平行四边形一边长为5，一条对角线长为6，则它的另一条对角线α的取值范围为（　　）

  A．1＜α＜11	B．4＜α＜16
  C．10＜α＜12	D．以上答案都不正确
  组卷：64引用：2难度：0.7

  解析

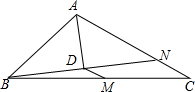• 4．在△ABC中，点M为BC的中点，AD平分∠BAC，且BD⊥AD于点D，延长BD交AC于点N若AB=4，DM=1，则AC的长为（　　）

  A．5

  B．6

  C．7

  D．8
  组卷：1213引用：11难度：0.6

  解析

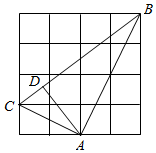• 5．在如图的网格中，每个小正方形的边长为1，A、B、C三点均在正方形格点上，若AD是△ABC的高，则AD的长为（　　）

  A．2 3

  B． 5

  C． 3

  D．2
  组卷：1193引用：15难度：0.7

  解析

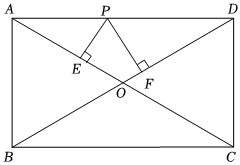• 6．已知：如图，矩形ABCD中，AB=5，BC=12，对角线AC、BD相交于点O，点P是线段AD上任意一点，且PE⊥AC于点E，PF⊥BD于点F，则PE+PF等于（　　）

  A．6

  B．5

  C． 60 13

  D． 60 11
  组卷：533引用：3难度：0.6

  解析

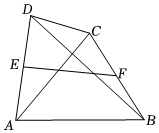• 7．如图，已知四边形ABCD中，AC⊥BD，AC=6，BD=8，点E、F分别是边AD、BC的中点，连接EF，则EF的长是（　　）

  A． 24

  B．5

  C． 32

  D．10
  组卷：2356引用：6难度：0.3

  解析

三、解答题

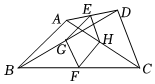• 22．已知：如图，在四边形ABCD中，AB与CD不平行，E，F，G，H分别是AD，BC，BD，AC的中点．
  （1）求证：四边形EGFH是平行四边形；
  （2）①当AB与CD满足条件

  时，四边形EGFH是菱形，在（1）的基础上此时判定菱形的依据是

  ．
  ②当AB与CD满足什么条件时，四边形EGFH是矩形？证明你的结论．
  组卷：474引用：6难度：0.6

  解析

• 23．按要求回答下列问题：
  发现问题．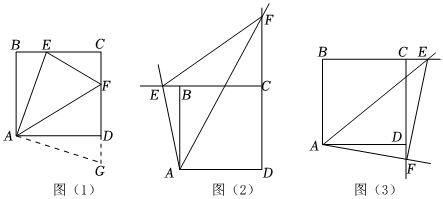
  
  （1）如图（1），在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF=45°，易证：EF=DF+BE．（不必证明）；
  （2）类比延伸
  ①如图（2），在正方形ABCD中，如果点E，F分别是边BC，CD延长线上的动点，且∠EAF=45°，则（1）中的结论还成立吗？请写出证明过程；
  ②如图（3），如果点E，F分别是边BC，CD延长线上的动点，且∠EAF=45°，则EF，BE，DF之间的数量关系是

  ．（不要求证明）
  （3）拓展应用：如图（1），若正方形的ABCD边长为6，

  AE

  =

  3

  5

  ，求EF的长．
  组卷：235引用：4难度：0.1

  解析