2022-2023学年湖南省长沙一中高三（下）月考数学试卷（七）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合M={x|2x+1＜3}，N={x|x＜a}，若M∩N=N，则实数a的取值范围为（　　）

  A．[1，+∞）

  B．[2，+∞）

  C．（-∞，1]

  D．（-∞，1）
  组卷：100引用：3难度：0.7

  解析

• 2．若实数x,y满足（x+i）（3+yi）=2+4i,则xy=（　　）

  A．-1

  B．1

  C．3

  D．-3
  组卷：12引用：2难度：0.8

  解析

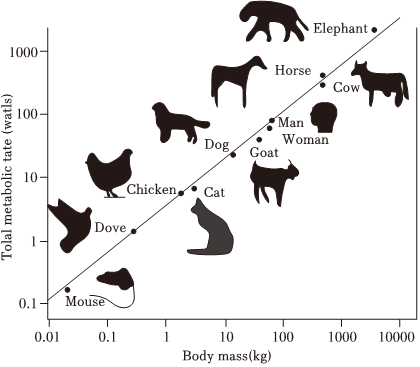• 3．1947年，生物学家Max Kleiber发表了一篇题为《body size and metabolic rate》的论文，在论文中提出了一个克莱伯定律：对于哺乳动物，其基础代谢率与体重的

  3

  4

  次幂成正比，即

  F

  =

  c

  0

  M

  3

  4

  ，其中F为基础代谢率，M为体重．若某哺乳动物经过一段时间生长，其体重为原来的10倍，则基础代谢率为原来的（　　）
  （参考数据：

  4

  10

  ≈

  1

  .

  7783

  ）

  A．5.4倍

  B．5.5倍

  C．5.6倍

  D．5.7倍
  组卷：82引用：2难度：0.8

  解析

• 4．已知函数f（x）=|x|+sin²x,设x₁，x₂∈R，则f（x₁）＞f（x₂）成立的一个必要不充分条件是（　　）

  A．x1＞x2

  B．x2＞x1

  C．x1+x2＞0

  D．|x1|＞x2
  组卷：24引用：1难度：0.7

  解析

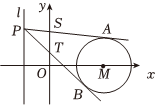• 5．如图，圆M：（x-2）²+y²=1，点P（-1，t）为直线l：x=-1上一动点，过点P引圆M的两条切线，切点分别为A，B；若两条切线PA，PB与y轴分别交于S，T两点，则|ST|的最小值为（　　）

  A． 1 2

  B． 2 2

  C．1

  D． 2
  组卷：138引用：2难度：0.5

  解析

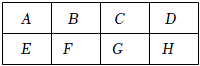• 6．某旅游景区有如图所示A至H共8个停车位，现有2辆不同的白色车和2辆不同的黑色车，要求相同颜色的车不停在同一行也不停在同一列，则不同的停车方法总数为（　　）

  A．288

  B．336

  C．576

  D．1680
  组卷：1124引用：9难度：0.7

  解析

• 7．在平面直角坐标系xOy中，已知过抛物线y²=4x焦点F的直线与抛物线相交于A，B两点，以AF，BF为直径的圆分别与x轴交于异于F的P，Q两点，若|PF|=2|FQ|，则线段|AB|的长为（　　）

  A． 5 2

  B． 7 2

  C． 9 2

  D． 13 2
  组卷：72引用：2难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步聚.

• 21．已知双曲线C：

  x

  2

  3

  -

  y

  2

  =

  1

  ．
  （1）若点P在曲线C上，点A，B分别在双曲线C的两渐近线l₁、l₂上，且点A在第一象限，点B在第四象限，若

  AP

  =

  λ

  PB

  ，

  λ

  ∈

  [

  1

  3

  ，

  2

  ]

  ，求△AOB面积的最大值；
  （2）设双曲线C的左、右焦点分别为F₁、F₂，过左焦点F₁作直线l交双曲线的左支于G、Q两点，求△GQF₂周长的取值范围．
  组卷：145引用：3难度：0.3

  解析

• 22．已知函数f（x）=（x+n）lnx.
  （1）若n=1，求函数g（x）=f（x）-k（x-1）（k＞2）的零点个数，并说明理由；
  （2）当n=0时，若方程f（x）=b有两个实根x₁，x₂，且x₁＜x₂，求证：be+1＜x₂-x₁＜

  e

  -

  3

  +

  2

  +

  3

  b

  2

  ．
  组卷：77引用：3难度：0.2

  解析