2022-2023学年广东省中山一中高一（下）期中数学试卷

一、选择题（本题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出最符合题目要求的一项）

• 1．为了营造浓厚的校园体育氛围，学校采用按比例分层抽样的方法从高一550人，高二500人，高三450人中抽取60人观看排球决赛，那么高一年级被抽取的人数为（　　）

  A．18

  B．20

  C．22

  D．30
  组卷：53引用：1难度：0.7

  解析

• 2．在空间中，下列说法正确的是（　　）

  A．垂直于同一直线的两条直线平行

  B．垂直于同一直线的两条直线垂直

  C．平行于同一平面的两条直线平行

  D．垂直于同一平面的两条直线平行
  组卷：259引用：7难度：0.7

  解析

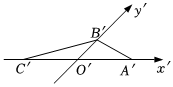• 3．如图所示，△A'B'C'是水平放置的△ABC的斜二测直观图，其中O'C'=O'A'=2O'B'=2，则以下说法正确的是（　　）

  A．△ABC是钝角三角形

  B．△ABC的面积是△A'B'C'的面积的2倍

  C．B点的坐标为 （ 0 ， 2 ）

  D．△ABC的周长是 4 + 4 2
  组卷：327引用：5难度：0.8

  解析

• 4．17世纪30年代，意大利数学家卡瓦列利在《不可分量几何学》一书中介绍了利用平面图形旋转计算球体体积的方法．如图，

  ˆ

  AEB

  是一个半圆，圆心为O，ABCD是半圆的外切矩形．以直线OE为轴将该平面图形旋转一周，记△OCD，阴影部分，半圆

  ˆ

  AEB

  所形成的几何体的体积分别为V₁，V₂，V₃，则下列说法正确的是（　　）

  A．V1+V2＜V3

  B．V1+V2＞V3

  C．V1＞V2

  D．V1=V2
  组卷：136引用：4难度：0.7

  解析

• 5．已知△ABC中，点M是线段BC的中点，

  AN

  =

  1

  4

  AM

  ，则

  BN

  =（　　）

  A． - 7 8 AB + 1 8 AC	B． - 2 3 AB + 1 12 AC
  C． - 7 4 AB + 1 4 AC	D． - 5 6 AB + 1 12 AC
  组卷：289引用：2难度：0.7

  解析

• 6．要得到

  y

  =

  sin

  x

  2

  的图象，只需将函数

  y

  =

  cos

  （

  x

  2

  -

  π

  4

  ）

  的图象（　　）

  A．向左平移 π 4 个单位长度	B．向右平移 π 4 个单位长度
  C．向左平移 π 2 个单位长度	D．向右平移 π 2 个单位长度
  组卷：390引用：4难度：0.7

  解析

• 7．已知函数f（x）=cosx,若A，B是锐角三角形的两个内角，则一定有（　　）

  A．f（sinA）＞f（sinB）	B．f（cosA）＞f（cosB）
  C．f（sinA）＞f（cosB）	D．f（cosA）＞f（sinB）
  组卷：281引用：3难度：0.6

  解析

四、解答题（本题共6小题，共70分.解答题应写出文字说明、证明过程和验算步骤）

• 21．如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，

  AB

  =

  BC

  =

  1

  2

  AD

  =

  2

  ，∠BAD=∠ABC=90°，O是AD的中点．
  （1）求证：平面PAC⊥平面POB；
  （2）点M在棱PC上，满足PM=λPC（0＜λ＜1），且三棱锥P-ABM的体积为

  3

  3

  ，求λ的值及二面角M-AB-D的正切值．
  组卷：560引用：6难度：0.5

  解析

• 22．在大力推进城镇化的旧房改造进程中，晓颖家旧房拆迁拿到一套新房外加一间店面．晓颖准备将店面改建成超市，遇到如下问题：如图所示，一条直角走廊宽为2米，现有一转动灵活的平板车希望能自如在直角走廊运行．平板车平板面为矩形ABEF，它的宽为1米．直线EF分别交直线AC，BC于M，N，过墙角D作DP⊥AC于P，DQ⊥BC于Q；请你结合所学知识帮晓颖解决如下问题：
  （1）若平板车卡在直角走廊内，且

  ∠

  CAB

  =

  θ

  ，

  （

  0

  ＜

  θ

  ＜

  π

  2

  ）

  ，试将平板面的长AB表示为θ的函数f（θ）；
  （2）证明：当0＜θ＜

  π

  2

  时，1＜sinθ+cosθ≤

  2

  ；
  （3）若平板车要想顺利通过直角走廊，其长度不能超过多少米？
  组卷：116引用：8难度：0.4

  解析