2023-2024学年黑龙江省大庆市萨尔图区东风中学高二(上)月考数学试卷(一)
发布:2024/8/31 17:0:8
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
-
1.若复数z满足
,则z在复平面内对应的点位于( )(1-i)z=(2-i)2组卷:109引用:4难度:0.8 -
2.已知
,a是单位向量,若b,则a⊥(a+3b)在a上的投影向量为( )b组卷:154引用:8难度:0.8 -
3.在空间中,l,m,n,a,b表示直线,α表示平面,则下列命题正确的是( )
组卷:17引用:3难度:0.7 -
4.调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图和“90后”从事互联网行业岗位分布条形图,则下列结论中一定正确的是( )
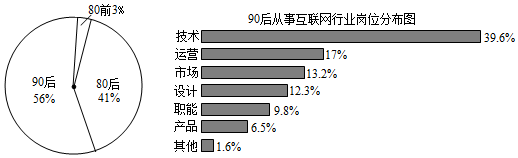 组卷:106引用:3难度:0.8
组卷:106引用:3难度:0.8 -
5.足球点球大战中,每队派出5人进行点球,假设甲队每人点球破门的概率都是
,乙队每人点球破门的概率都是34,若甲队进4球的概率为P1,乙队队进3球的概率为P2,则( )23组卷:91引用:3难度:0.8 -
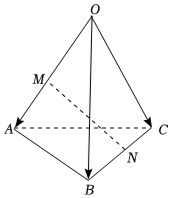 6.如图,空间四边形OABC中,=OA,a=OB,b=OC,点M在c上,且满足OA=2OM,点N为BC的中点,则MA=( )NM组卷:350引用:15难度:0.7
6.如图,空间四边形OABC中,=OA,a=OB,b=OC,点M在c上,且满足OA=2OM,点N为BC的中点,则MA=( )NM组卷:350引用:15难度:0.7 -
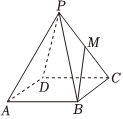 7.如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB,AD的夹角都等于60°.若M是PC的中点,则=( )|BM|组卷:61引用:3难度:0.6
7.如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB,AD的夹角都等于60°.若M是PC的中点,则=( )|BM|组卷:61引用:3难度:0.6
四、解答题(本大题共6小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
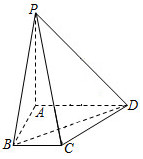 21.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,AD=2BC,M为PD的中点.
21.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,AD=2BC,M为PD的中点.
(Ⅰ)证明:CM∥平面PAB;
(Ⅱ)若△PBD是边长为2的等边三角形,求点C到平面PBD的距离.组卷:69引用:2难度:0.6 -
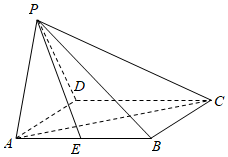 22.如图,四棱锥P-ABCD的底面ABCD为菱形,面PAD⊥面ABCD,PA=PD=5,AD=6,∠DAB=60°,E为AB的中点.
22.如图,四棱锥P-ABCD的底面ABCD为菱形,面PAD⊥面ABCD,PA=PD=5,AD=6,∠DAB=60°,E为AB的中点.
(1)证明:AC⊥PE;
(2)求二面角D-PA-B的余弦值.组卷:127引用:6难度:0.5


