2022-2023学年安徽省合肥市、淮南市部分学校高二（上）开学数学试卷

一、选择题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

• 1．已知集合A={1，2，3，4，5}，B={x|-1≤x≤2}，则A∩（∁_RB）=（　　）

  A．{1}

  B．{1，2}

  C．{3，4，5}

  D．{2，3，4，5}
  组卷：9引用：2难度：0.7

  解析

• 2．在平面直角坐标系xOy中，角α的终边与单位圆交于点

  （

  7

  4

  ，-

  3

  4

  ）

  ，则

  sin

  （

  3

  π

  2

  +

  2

  α

  ）

  =（　　）

  A． - 1 8

  B． 1 8

  C． - 3 7 8

  D． - 7 4
  组卷：34引用：3难度：0.7

  解析

• 3．已知幂函数f（x）=（m²-4m-4）x^m在（0，+∞）上单调递增，则f（2）=（　　）

  A． 1 2

  B．2

  C． 1 32

  D．32
  组卷：16引用：3难度：0.7

  解析

• 4．已知

  a

  =

  lo

  g

  1

  2

  3

  ，

  b

  =

  lo

  g

  5

  2

  ，

  c

  =

  4

  -

  0

  .

  3

  ，则（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．a＜b＜c

  D．a＜c＜b
  组卷：6引用：2难度：0.7

  解析

• 5．甲、乙两名志愿者均打算高考期间去A，B，C三个考点中的一个考点做服务，甲去A，B考点做服务的概率分别为0.4，0.3，乙去B，C考点做服务的概率分别为0.5，0.2，则甲、乙不去同一考点做服务的概率为（　　）

  A．0.26

  B．0.33

  C．0.67

  D．0.74
  组卷：23引用：3难度：0.7

  解析

• 6．如图为2022年北京冬奥会首钢滑雪大跳台示意图，为测量大跳台最高点P距地面的距离，小明同学在场馆内的点A测得P的仰角为30°，∠ABO=75°，∠BAO=60°，AB=60（单位：m），点A，B，O在同一水平地面上，则大跳台最高高度OP=（　　）
  

  A． （ 30 + 10 3 ） m

  B． 30 2 m

  C． （ 10 2 + 10 6 ） m

  D． 30 3 m
  组卷：8引用：2难度：0.6

  解析

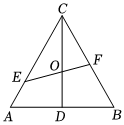• 7．如图，在△ABC中，D是AB的中点，O是CD上一点，且

  CO

  =

  2

  OD

  ，过点O作一条直线与边AC，BC分别相交于点E，F，若

  CE

  =

  3

  4

  CA

  ，

  CF

  =

  μ

  CB

  ，则μ=（　　）

  A． 3 4

  B． 3 5

  C． 1 2

  D． 4 5
  组卷：38引用：2难度：0.5

  解析

四、解答题（本题共6小题，第17题10分，第18～22题每题12分，共70分。解答应写出文字说明、证明过程或演算步骤。）

• 21．在①

  cos

  B

  cos

  C

  =

  b

  2

  a

  -

  c

  ；②

  1

  tan

  A

  +

  1

  tan

  B

  =

  2

  3

  sin

  C

  3

  sin

  A

  ；③设△ABC的面积为S，且4

  3

  S+3（b²-a²）=3c²．这三个条件中任选一个，补充在下面的横线上．并加以解答．在△ABC中．角A，B，C的对边分别为a,b,c,且_____．
  （1）求角B的大小；
  （2）若b=2

  3

  ，0＜B＜

  π

  2

  ，求钝角△ABC的周长的取值范围．
  （如果选择多个条件分别解答，按第一个解答计分）
  组卷：62引用：2难度：0.6

  解析

• 22．已知函数f（x）=

  1

  4

  x

  +

  λ

  +1．
  （1）若λ=1，求证：函数f（x）的图象关于点（0，

  3

  2

  ）中心对称；
  （2）若λ=0，且关于x的不等式|f（x）+m•2^-x|≤5在[0，+∞）上恒成立，求实数m的取值范围．
  组卷：29引用：1难度：0.4

  解析