2022-2023学年黑龙江省牡丹江第二高级中学高一（下）期末数学试卷

一、选择题：本大题共8小题；每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

• 1．在复平面内，复数3i-2对应的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：49引用：3难度：0.9

  解析

• 2．在平行四边形ABCD中，

  AB

  +

  AD

  等于（　　）

  A． AC

  B． BD

  C． BC

  D． CD
  组卷：504引用：3难度：0.9

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  4

  ，

  m

  ）

  ，且

  a

  ⊥

  b

  ，则m=（　　）

  A．8

  B．2

  C．-2

  D．-8
  组卷：289引用：6难度：0.8

  解析

• 4．若

  a

  =（2，0，1），

  b

  =（-3，1，-1），

  c

  =（1，1，0），则

  a

  +2

  b

  -3

  c

  =（　　）

  A．（-1，-2，0）

  B．（-7，-1，0）

  C．（-7，-1，1）

  D．（-7，-1，-1）
  组卷：398引用：10难度：0.8

  解析

• 5．设正方体的棱长为

  3

  ，则它的外接球的表面积为（　　）

  A． 9 2 π

  B． 9 4 π

  C．9π

  D．3π
  组卷：96引用：2难度：0.7

  解析

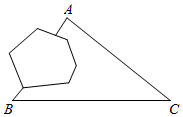• 6．如图，在高速公路建设中，要确定隧道AB的长度，工程人员测得隧道两端的A，B两点到C点的距离分别为AC=3km,BC=4km,且∠ACB=60°，则隧道AB长度为（　　）

  A．2 2 km

  B． 11 km

  C．2 3 km

  D． 13 km
  组卷：149引用：2难度：0.8

  解析

• 7．下列命题中为真命题的是（　　）

  A．向量 AB 与 BA 的长度相等

  B．空间向量就是空间中的一条有向线段

  C．若将空间中所有的单位向量移到同一个起点，则它们的终点构成一个圆

  D．不相等的两个空间向量的模必不相等
  组卷：128引用：7难度：0.7

  解析

四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤.

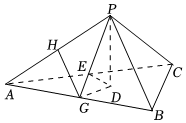• 21．如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．作GH∥PB交PA于H．
  （1）证明：G是AB的中点；
  （2）证明：GH⊥面PAC；
  （3）过点E作EF⊥面PAC，F为垂足，求三棱锥P-DEF的外接球体积．
  组卷：133引用：2难度：0.4

  解析

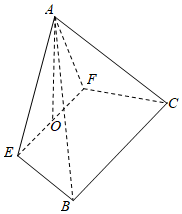• 22．如图，将边长为4的等边三角形ABC沿与边BC平行的直线EF折起，使得平面AEF⊥平面BCEF，O为EF的中点．
  （1）求平面AEF与平面AEB所成角的余弦值；
  （2）若BE⊥平面AOC，试求折痕EF的长；
  （3）当点O到平面ABC距离最大时，求折痕EF的长．
  组卷：273引用：5难度：0.3

  解析