2023-2024学年广东省惠州市高三（上）第一次调研数学试卷

一、单项选择题：本题共8小题，每小题满分40分，共40分。在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分。

• 1．设U={x|x是不大于6的正整数}，A={1，2，3}，B={3，5}，求∁_U（A∪B）=（　　）

  A．∅	B．{4，6}
  C．{1，2，3，5}	D．{1，2，3，4，5，6}
  组卷：252引用：6难度：0.9

  解析

• 2．设复数z满足z（1-i）=1+i,则z的虚部为（　　）

  A．-1

  B．1

  C．i

  D．-i
  组卷：96引用：7难度：0.8

  解析

• 3．若（x+2）⁴=a₄x⁴+a₃x³+a₂x²+a₁x+a₀，则a₄-a₃+a₂-a₁+a₀=（　　）

  A．1

  B．-1

  C．15

  D．-15
  组卷：99引用：2难度：0.9

  解析

• 4．设a∈R，则“a＞1”是“a²＞1”的（　　）

  A．充分非必要条件	B．必要非充分条件
  C．充要条件	D．既非充分也非必要条件
  组卷：5263引用：50难度：0.9

  解析

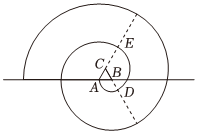• 5．蚊香具有悠久的历史，我国蚊香的发明与古人端午节的习俗有关．如图为某校数学社团用数学软件制作的“蚊香”．画法如下：在水平直线上取长度为1的线段AB，作一个等边三角形ABC，然后以点B为圆心，AB为半径逆时针画圆弧交线段CB的延长线于点D（第一段圆弧），再以点C为圆心，CD为半径逆时针画圆弧交线段AC的延长线于点E，再以点A为圆心，AE为半径逆时针画圆弧……以此类推，当得到的“蚊香”恰好有11段圆弧时，“蚊香”的长度为（　　）

  A．14π

  B．18π

  C．30π

  D．44π
  组卷：283引用：9难度：0.7

  解析

• 6．甲乙两位游客慕名来到惠州旅游，准备分别从惠州西湖、博罗罗浮山、龙门南昆山、惠东盐洲岛和大亚湾红树林5个景点中各随机选择其中一个景点游玩，记事件A：甲和乙选择的景点不同，事件B：甲和乙恰好一人选择罗浮山，则P（B|A）=（　　）

  A． 1 5

  B． 2 5

  C． 9 25

  D． 9 20
  组卷：66引用：1难度：0.8

  解析

• 7．设O为坐标原点，F₁，F₂是双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦点，已知双曲线C的离心率为

  3

  ，过F₂作C的一条渐近线的垂线，垂足为P，则

  |

  P

  F

  1

  |

  |

  OP

  |

  =（　　）

  A． 6

  B．2

  C． 3

  D． 6 2
  组卷：181引用：5难度：0.6

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左顶点为A，上顶点为B，右焦点为F（1，0），O为坐标原点，线段OA的中点为D，且|BD|=|DF|．
  （1）求C的方程；
  （2）已知点M，N均在直线x=2上，以MN为直径的圆经过O点，圆心为点T，直线AM，AN分别交椭圆C于另一点P，Q，证明：直线PQ与直线OT垂直．
  组卷：243引用：10难度：0.4

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  lnx

  -

  a

  （

  x

  -

  1

  x

  ）

  ，a＞0．
  （1）讨论f（x）极值点的个数；
  （2）若f（x）恰有三个零点t₁，t₂，t₃（t₁＜t₂＜t₃）和两个极值点x₁，x₂（x₁＜x₂）．
  （ⅰ）证明：f（x₁）+f（x₂）=0；
  （ⅱ）若m＜n,且mlnm=nlnn,证明：

  （

  1

  -

  m

  ）

  e

  -

  m

  t

  1

  t

  2

  t

  3

  ＞

  n

  （

  lnn

  +

  1

  ）

  ．
  组卷：275引用：7难度：0.6

  解析