当前位置：试卷中心 > 试卷详情

2023-2024学年浙江省嘉兴第五高级中学高二（上）第一次段考数学试卷

发布：2024/8/30 2:0:8

1．直线
3
x
-
y
-
4
=
0
的倾斜角是（　　）
A．30° B．60° C．120° D．150°
组卷：79引用：19难度：0.8
解析
2．圆
（
x
-
1
）
2
+
（
y
+
3
）
2
=
1
的圆心坐标是（　　）
A．
（
1
，
3
）
B．
（
-
1
，
3
）
C．
（
1
，-
3
）
D．
（
-
1
，-
3
）
组卷：118引用：2难度：0.7
解析
3．过点A（1，4）的直线的方向向量为
m
=
（
1
，
2
）
，则该直线方程为（　　）
A．2x-y+2=0 B．2x+y-6=0 C．x-2y+7=0 D．2x+2y-10=0
组卷：382引用：12难度：0.8
解析
4．圆x²+y²=1与圆（x-3）²+（y-4）²=16的位置关系是（　　）
A．相交 B．内切 C．外切 D．相离
组卷：74引用：5难度：0.9
解析
5．若直线x+（1+m）y-2=0和直线mx+2y+4=0平行，则m的值为（　　）
A．1 B．-2 C．1或-2 D．
-
2
3
组卷：6528引用：37难度：0.9
解析
6．当点P在圆x²+y²=1上变动时，它与定点Q（-3，0）的连结线段PQ的中点的轨迹方程是（　　）
A．（x+3）²+y²=4 B．（x-3）²+y²=4
C．（2x-3）²+4y²=1 D．（2x+3）²+4y²=1
组卷：332引用：15难度：0.7
解析
7．已知两点A（-4，8），B（2，4），点C在直线y=x+1上，则|AC|+|BC|的最小值为（　　）
A．
2
13
B．9 C．
74
D．10
组卷：577引用：6难度：0.7
解析

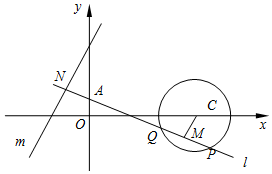21．已知圆C：（x-3）²+y²=1与直线m：3x-y+6=0，动直线l过定点A（0，1）．
（1）若直线l与圆C相切，求直线l的方程；
（2）若直线l与圆C相交于P、Q两点，点M是PQ的中点，直线l与直线m相交于点N．探索
AM
•
AN
是否为定值，若是，求出该定值；若不是，请说明理由．
组卷：243引用：19难度：0.5
解析
22．已知直线方程为（2-m）x+（2m+1）y+3m+4=0，其中m∈R．
（1）求直线恒过定点的坐标．当m变化时，求点Q（3，4）到直线的距离的最大值及此时的直线方程；
（2）若直线分别与x轴、y轴的负半轴交于A，B两点，求△AOB面积的最小值及此时的直线方程．
组卷：70引用：6难度：0.6
解析