当前位置：试卷中心 > 试卷详情

2022-2023学年云南省玉溪市高一（下）期末数学试卷

发布：2024/6/11 8:0:9

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知集合A={x|x-2≤0}，B={x|y=lnx}，则A∩B=（　　）
A．（-∞，0）∪[2，+∞） B．[2，+∞）
C．（0，2] D．[0，2]
组卷：28引用：1难度：0.8
解析
2．下列说法正确的是（　　）
A．若a＞b＞0，则ac＞bc B．若a＞b,则|a|＞|b|
C．若a＜b＜0，则a²＞ab D．若a＞b＞c,则
a
b
＞
a
+
c
b
+
c
组卷：491引用：13难度：0.9
解析
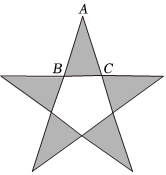3．17世纪德国著名的天文学家开普勒曾经这样说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割．如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿．”黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是一个顶角为36°的等腰三角形（另一种是顶角为108°的等腰三角形）．例如，五角星由五个黄金三角形与一个正五边形组成，如图所示，在其中一个黄金△ABC中，
BC
AC
=
5
-
1
2
．根据这些信息，可得sin18°=（　　）
A．
5
-
1
2
B．
5
-
1
4
C．
5
+
1
4
D．
5
+
1
8
组卷：41引用：1难度：0.7
解析
4．若数据x₁，x₂，…，x_n的平均数为5，方差为5，则3x₁+4，3x₂+4，…，3x_n+4的平均数和方差分别为（　　）
A．5，5 B．15，15 C．19，19 D．19，45
组卷：70引用：1难度：0.7
解析
5．已知两个单位向量
e
1
，
e
2
的夹角为60°，且满足
e
1
⊥（λ
e
2
-
e
1
），则实数λ的值是（　　）
A．-2 B．2 C．
2
D．1
组卷：76引用：2难度：0.9
解析
6．在三棱锥P-ABC中，PA⊥平面ABC，
∠
BAC
=
π
2
，AB=AC=AP=2，则三棱锥外接球的表面积为（　　）
A．4π B．12π C．
40
3
π
D．16π
组卷：110引用：3难度：0.5
解析
7．
3
tan
10
°
+
3
tan
20
°
+
tan
10
°
tan
20
°
=（　　）
A．1 B．
3
C．3 D．
2
3
组卷：118引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

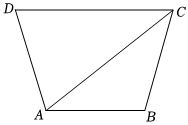21．如图，在梯形ABCD中，AB∥CD，AD=BC=AB=2，CD=AC．
（Ⅰ）求CD；
（Ⅱ）平面内点P在直线CD的上方，且满足2∠DPC=5∠ACB，求DP+CP的最大值．
组卷：14引用：1难度：0.5
解析
22．一艘船上的某种液体漏到一片海域中，为了治污，根据环保部门的建议，现决定在该片海域中投放一种与污染液体发生化学反应的药剂，已知每投放a（2≤a≤6，a∈R）个单位的药剂，它在海水中释放的浓度y（克/升）随着时间x（天）变化的函数关系式近似为y=a•f（x）（投放当天x=0），其中
f
（
x
）
=
16
8
-
x
-
1
（
0
≤
x
≤
4
）
5
-
1
2
x
（
4
＜
x
≤
10
）
，若多次投放，则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和．根据经验，当海水中药剂的浓度不低于6（克/升）时，它才能起到有效治污的作用．
（Ⅰ）若一次投放2个单位的药剂，则有效治污时间可达几天？
（Ⅱ）若第一次投放4个单位的药剂，6天后再投放（第二次投放）a个单位的药剂，要使第二次投放后的5天（含投放当天）能够持续有效治污，试求a的最小值．
组卷：55引用：3难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（-∞，0）∪[2，+∞）	B．[2，+∞）
C．（0，2]	D．[0，2]

A．若a＞b＞0，则ac＞bc	B．若a＞b,则\|a\|＞\|b\|
C．若a＜b＜0，则a²＞ab	D．若a＞b＞c,则 a b ＞ a + c b + c

2022-2023学年云南省玉溪市高一（下）期末数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知集合A={x|x-2≤0}，B={x|y=lnx}，则A∩B=（ ）

2．下列说法正确的是（ ）

4．若数据x1，x2，…，xn的平均数为5，方差为5，则3x1+4，3x2+4，…，3xn+4的平均数和方差分别为（ ）

5．已知两个单位向量e1，e2的夹角为60°，且满足e1⊥（λe2-e1），则实数λ的值是（ ）

6．在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=π2，AB=AC=AP=2，则三棱锥外接球的表面积为（ ）

7．3tan10°+3tan20°+tan10°tan20°=（ ）

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

21．如图，在梯形ABCD中，AB∥CD，AD=BC=AB=2，CD=AC．（Ⅰ）求CD；（Ⅱ）平面内点P在直线CD的上方，且满足2∠DPC=5∠ACB，求DP+CP的最大值．

1．已知集合A={x|x-2≤0}，B={x|y=lnx}，则A∩B=（　　）

2．下列说法正确的是（　　）

4．若数据x₁，x₂，…，x_n的平均数为5，方差为5，则3x₁+4，3x₂+4，…，3x_n+4的平均数和方差分别为（　　）

5．已知两个单位向量
e
1
，
e
2
的夹角为60°，且满足
e
1
⊥（λ
e
2
-
e
1
），则实数λ的值是（　　）

6．在三棱锥P-ABC中，PA⊥平面ABC，
∠
BAC
=
π
2
，AB=AC=AP=2，则三棱锥外接球的表面积为（　　）

7．
3
tan
10
°
+
3
tan
20
°
+
tan
10
°
tan
20
°
=（　　）

21．如图，在梯形ABCD中，AB∥CD，AD=BC=AB=2，CD=AC．
（Ⅰ）求CD；
（Ⅱ）平面内点P在直线CD的上方，且满足2∠DPC=5∠ACB，求DP+CP的最大值．