2023-2024学年宁夏银川市灵武一中高二(上)第一次月考数学试卷
发布:2024/9/7 4:0:8
一、单选题
-
1.直线l经过点(2,3),且倾斜角α=45°,则直线l的方程为( )
组卷:302引用:10难度:0.8 -
2.已知
=(1,n,-2),a=(2,4,m),且b,则m+n=( )a∥b组卷:233引用:4难度:0.8 -
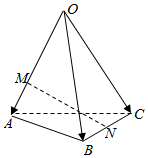 3.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9
3.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9 -
4.下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是( )
组卷:900引用:56难度:0.9 -
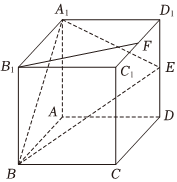 5.如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,点F在棱C1D1上,且,若B1F∥平面A1BE,则λ=( )D1F=λD1C1组卷:255引用:9难度:0.8
5.如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,点F在棱C1D1上,且,若B1F∥平面A1BE,则λ=( )D1F=λD1C1组卷:255引用:9难度:0.8 -
6.在正方体ABCD-A1B1C1D1中,M是线段C1D1(不含端点)上的动点,N为BC的中点,则( )
组卷:175引用:5难度:0.6 -
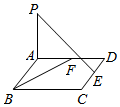 7.如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF:FD的比值为( )组卷:45引用:3难度:0.7
7.如图,PA⊥平面ABCD,四边形ABCD为正方形,E是CD的中点,F是AD上一点,当BF⊥PE时,AF:FD的比值为( )组卷:45引用:3难度:0.7
四、解答题
-
 21.四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
21.四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥底面ABCD,PB与底面ABCD所成的角为60°,E是PB的中点.
(1)求异面直线DE与PA所成角的余弦值;
(2)证明:OE∥平面PAD,并求点E到平面PAD的距离.组卷:93引用:15难度:0.6 -
22.如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.
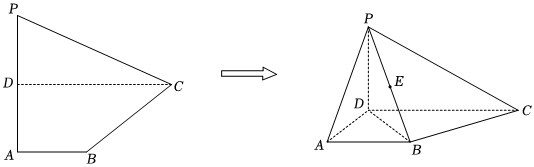
(1)证明:平面PBD⊥平面PBC;
(2)在线段BD上是否存在一点F,使得EF⊥平面PBC?若存在,请确定点F的位置;若不存在,请说明理由.组卷:38引用:4难度:0.5


