当前位置：试卷中心 > 试卷详情

2022-2023学年广东省惠城区东莞中学、惠州一中、深圳实验中学、珠海一中、中山纪念中学高二（下）月考数学试卷

发布：2024/5/20 8:0:9

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设函数f（x）=x²+3x,则
lim
Δ
x
→
0
f
（
1
+
Δ
x
）
-
f
（
1
）
Δ
x
=（　　）
A．5 B．-5 C．2 D．-2
组卷：53引用：3难度：0.8
解析
2．（1+x²）（1-x）⁸展开式中x³的系数为（　　）
A．56 B．-56 C．64 D．-64
组卷：168引用：2难度：0.7
解析
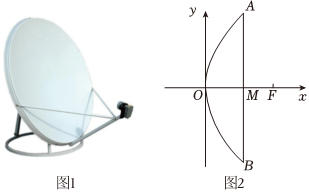3．一种卫星接收天线（如图1），其曲面与轴截面的交线可视为抛物线的一部分（如图2），已知该卫星接收天线的口径AB=8米，深度MO=1米，信号处理中心F位于焦点处，以顶点o为坐标原点，建立如图2所示的平面直角坐标系xOy,则该抛物线的方程为（　　）
A．y²=8x B．y²=16x C．y=8x² D．y=16x²
组卷：31引用：1难度：0.7
解析
4．各项均为正数的等差数列{a_n}的前n项和是S_n，若
a
2
9
-
a
7
+
1
2
a
5
=
0
，则S₁₇的值为（　　）
A．
7
2
B．
17
2
C．
7
3
D．
17
3
组卷：132引用：3难度：0.8
解析
5．一个盒子里装有大小，材质均相同的黑球10个，红球12个，白球3个，从中任取3个，其中白球的个数记为X，则等于
C
1
3
C
2
22
+
C
3
22
C
3
25
的是（　　）
A．P（X＞2） B．P（0＜X＜2） C．P（X≤1） D．P（X＞1）
组卷：59引用：3难度：0.5
解析
6．将诗集《诗经》、《唐诗三百首》，戏剧《牡丹亭》，四大名著《红楼梦》、《西游记》、《三国演义》、《水浒传》7本书放在一排，下面结论成立的是（　　）
A．戏剧放在中间的不同放法有7!种
B．诗集相邻的不同放法有6!种
C．四大名著互不相邻的不同放法有
A
4
4
A
3
5
种
D．四大名著不放在两端的不同放法有6×5!种
组卷：43引用：1难度：0.7
解析
7．已知定义在R上的函数f（x）的导函数为f'（x），且对任意x∈R都有f′（x）＞2，f（2）=0，则不等式f（x）-2x+4＞0的解集为（　　）
A．（2，+∞） B．（1，+∞） C．（-∞，1） D．（-∞，2）
组卷：100引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤．

21．如图，已知椭圆
C
：
x
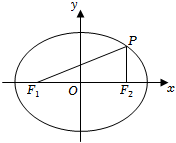2
a
2
+
y
2
=
1
（
a
＞
1
）
，其左、右焦点分别为F₁，F₂，过右焦点F₂且垂直于x轴的直线交椭圆于第一象限的点P，且
sin
∠
P
F
1
F
2
=
1
3
．
（1）求椭圆C的方程；
（2）过点
S
（
0
，-
1
3
）
且斜率为k的动直线l交椭圆于A，B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出点M的坐标；若不存在，说明理由．
组卷：373引用：5难度：0.4
解析
22．已知函数f（x）=lnx-
1
2
ax²+（a-1）x（a∈R，a≠0）．
（1）当a＜-1时，求函数f（x）的单调递增区间；
（2）记函数F（x）的图象为曲线C，设点A（x₁，y₁）、B（x₂，y₂）是曲线C上两个不同点，如果曲线C上存在M（x₀，y₀），使得：①
x
0
=
x
1
+
x
2
2
；②曲线C在点M处的切线平行于直线AB，则称函数F（x）存在“中值相依切线”．试问：函数f（x）是否存在中值相依切线，说明理由．
组卷：42引用：1难度：0.4
解析