2023-2024学年四川省内江市威远中学高二（上）第一次月考数学试卷

一、单选题：本大题共8小题，每小题5分，共40分.每个小题只有一个选项符合题目要求.

• 1．下列说法正确的是（　　）

  A．三个点可以确定一个平面

  B．若直线a在平面α外，则a与α无公共点

  C．用平行于底面的平面截正棱锥所得的棱台是正棱台

  D．斜棱柱的侧面不可能是矩形
  组卷：164引用：5难度：0.7

  解析

• 2．用斜二测画法画一个水平放置的平面图形的直观图是一个底角为45°，腰长为2，上底长为1的等腰梯形，则该平面图形的面积等于（　　）

  A． 2 + 2 2

  B． 4 + 2 2

  C． 4 + 4 2

  D． 8 + 4 2
  组卷：95引用：4难度：0.7

  解析

• 3．已知某圆台的高为2

  2

  ，上底面半径为1，下底面半径为2，则其侧面展开图的面积为（　　）

  A．9π

  B．6 2 π

  C．9 2 π

  D．8π
  组卷：308引用：5难度：0.8

  解析

• 4．空间不重合的三个平面可以把空间分成（　　）

  A．4或6或7个部分	B．4或6或7或8个部分
  C．4或7或8个部分	D．6或7或8个部分
  组卷：131引用：3难度：0.5

  解析

• 5．已知某圆台的高为

  2

  2

  ，上底面半径为1，下底面半径为2，则其侧面面积为（　　）

  A．9π

  B． 6 2 π

  C． 9 2 π

  D．8π
  组卷：76引用：1难度：0.9

  解析

• 6．在△ABC中，AB=BC=AC=2，将△ABC绕直线AB旋转一周，得到的旋转体的表面积为（　　）

  A． 2 3 π

  B． 4 3 π

  C． 8 3 π

  D． 16 3 π
  组卷：111引用：2难度：0.8

  解析

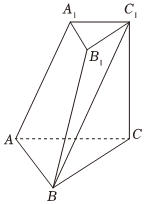• 7．三棱台ABC-A₁B₁C₁中，两底面△ABC和△A₁B₁C₁分别是边长为2和1的等边三角形，CC₁⊥平面ABC．若CC₁=2，则异面直线AC与BC₁所成角的余弦值为（　　）

  A． 14 4

  B． 7 7

  C． 2 4

  D． 2 2
  组卷：159引用：8难度：0.6

  解析

四、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

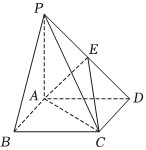• 21．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AC交BD于点O，E是PD上一点且PB∥平面ACE
  （1）证明：E为PD的中点；
  （2）在线段PA上是否存在点F，使得平面OEF∥平面PBC，若存在，请给出点F的位置，并证明，若不存在，请说明理由．
  组卷：192引用：2难度：0.7

  解析

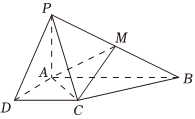• 22．已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中点．
  （1）证明：BC⊥平面PAC；
  （2）判断直线CM与平面PAD的位置关系，并证明你的结论；
  （3）求二面角A-MC-B的余弦值．
  组卷：291引用：9难度：0.5

  解析