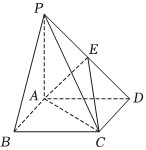
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC交BD于点O,E是PD上一点且PB∥平面ACE
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC交BD于点O,E是PD上一点且PB∥平面ACE
(1)证明:E为PD的中点;
(2)在线段PA上是否存在点F,使得平面OEF∥平面PBC,若存在,请给出点F的位置,并证明,若不存在,请说明理由.
【考点】平面与平面平行.
【答案】(1)证明见解析;(2)存在,F为PA中点.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/21 2:0:8组卷:195引用:2难度:0.7
相似题
-
 1.如图,正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.
1.如图,正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.
(1)求证:直线MN∥平面EFDB;
(2)求证:平面AMN∥平面EFDB.发布:2024/12/29 9:0:1组卷:188引用:3难度:0.3 -
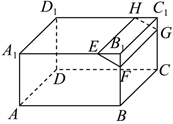 2.如图,在长方体ABCD-A1B1C1D1中,,则下列说法错误的是( )A1EEB1=BFFB1=CGGC1=D1HHC1=2发布:2024/11/30 13:0:1组卷:436引用:5难度:0.5
2.如图,在长方体ABCD-A1B1C1D1中,,则下列说法错误的是( )A1EEB1=BFFB1=CGGC1=D1HHC1=2发布:2024/11/30 13:0:1组卷:436引用:5难度:0.5 -
3.已知平面α与平面β间的距离为3,定点A∈α,设集合S={B∈β|AB=5},则S表示的曲线的长度为( )
发布:2024/10/7 1:0:1组卷:50引用:3难度:0.7


