2022-2023学年浙江省舟山市定海五中九年级（上）月考数学试卷（11月份）

一、选择题（本大题共10小题，每小题3分，每小题仅有一个正确选项，共30分）

• 1．如果x：y=1：2，那么下列各式不一定成立的是（　　）

  A． x + y y = 3 2

  B． x - y y = - 1 2

  C． 2 x y = 1

  D． x + 1 y + 1 = 2 3
  组卷：25引用：3难度：0.7

  解析

• 2．掷两个质地均匀的正方体骰子，则两次点数相同的概率是（　　）

  A． 1 6

  B． 1 36

  C． 1 12

  D． 1 3
  组卷：9引用：1难度：0.5

  解析

• 3．将函数y=x²+6x+7进行配方正确的结果应为（　　）

  A．y=（x+3）2+2

  B．y=（x-3）2+2

  C．y=（x+3）2-2

  D．y=（x-3）2-2
  组卷：483引用：24难度：0.9

  解析

• 4．二次函数y=（x-3）（x+5）的图象的对称轴是（　　）

  A．直线x=3

  B．直线x=-5

  C．直线x=-1

  D．直线x=1
  组卷：1469引用：14难度：0.7

  解析

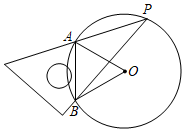• 5．如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，连结AO，BO，则∠AOB的度数是（　　）

  A．30°

  B．60°

  C．80°

  D．90°
  组卷：1039引用：17难度：0.5

  解析

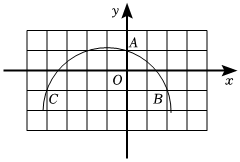• 6．如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C均在格点（两条网格线的交点叫格点）上，以点O为原点建立平面直角坐标系，则过A，B，C三点的圆的圆心坐标为（　　）

  A．（-1，-1）

  B．（-2，-1）

  C．（-1，-2）

  D．（-2，-2）
  组卷：441引用：4难度：0.7

  解析

• 7．给出下列结论：
  ①任意两个等边三角形相似
  ②顶角对应相等的两个等腰三角形相似
  ③两条边对应成比例的两个直角三角形相似
  其中正确的是（　　）

  A．①②

  B．①③

  C．②③

  D．①②③
  组卷：87引用：2难度：0.7

  解析

• 8．小高发现，用微波炉加工爆米花时，时间太短，一些颗粒没有充分爆开，时间太长，就糊了．如果将爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率p与加工时间t（单位：分钟）满足的函数关系p=at²+bt+c（a、b、c是常数），小高记录了三次实验的数据（如图）．根据上述函数模型和实验数据，可以得到最佳加工时间为（　　）
  

  A．3.50分钟

  B．3.75分钟

  C．4.00分钟

  D．4.25分钟
  组卷：650引用：11难度：0.5

  解析

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

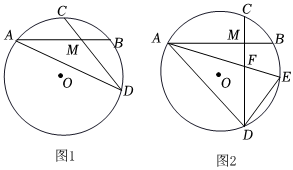• 23．已知：⊙O的两条弦AB，CD相交于点M，且AB=CD．
  （1）如图1，连接AD．求证：AM=DM．
  （2）如图2，若AB⊥CD，点E为弧BD上一点，

  ˆ

  BE

  =

  ˆ

  BC

  =α°，AE交CD于点F，连接AD、DE．
  ①求∠E的度数（用含α的代数式表示）．
  ②若DE=7，AM+MF=17，求△ADF的面积．
  组卷：451引用：3难度：0.5

  解析

• 24．平面直角坐标系中，抛物线y=-

  1

  4

  x

  2

  +bx+c与直线KB交于点B（2，0），K（-12，-14），与y轴交于点C．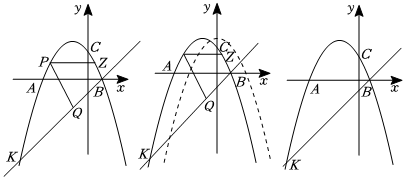
  
  （1）求抛物线的函数表达式及顶点坐标；
  （2）如图1，连接BC，点P是线段BK上方抛物线上的一个动点，过点P作PZ∥x轴交CB于点Z，过点P作PQ∥CB交直线KB于点Q，求

  6

  5

  5

  PQ+PZ的最大值及此时点P的坐标；
  （3）如图2，在（2）的条件下，将该抛物线向下平移

  3

  8

  个单位，向右平移3个单位，使得P点对应点P'．点S是新抛物线对称轴上一点，在平面上否存在一点N，使以P'、S、A、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
  组卷：41引用：2难度：0.5

  解析