已知：⊙O的两条弦AB，CD相交于点M，且AB=CD．
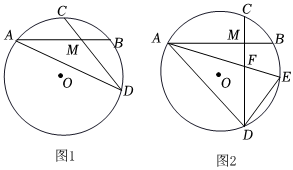
（1）如图1，连接AD．求证：AM=DM．
（2）如图2，若AB⊥CD，点E为弧BD上一点，ˆBE=ˆBC=α°，AE交CD于点F，连接AD、DE．
①求∠E的度数（用含α的代数式表示）．
②若DE=7，AM+MF=17，求△ADF的面积．
ˆ
BE
ˆ
BC
【考点】圆的综合题．
【答案】（1）证明见解答；
（2）①90°-α，②42．
（2）①90°-
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 15:0:2组卷：451引用：3难度：0.5
相似题
-
1．问题提出：
（1）我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就．小林用边长为10的正方形ABCD制作了一个“弦图”：如图①，在正方形ABCD内取一点E，使得∠BEC=90°，作DF⊥CE，AG⊥DF，垂足分别为F、G，延长BE交AG于点H．若EH=2，求tan∠BCE；
问题解决：
（2）如图②，四边形ABCD是公园中一块空地，AB=BC=50米，AD=CD，∠ABC=90°，∠D=60°，空地中有一段半径为50米的弧形道路（即），现准备在ˆAC上找一点P，将弧形道路改造为三条直路（即PA、PB、PC），并要求∠BPC=90°，三条直路将空地分割为△ABP、△BCP和四边形APCD三个区域，用来种植不同的花草．ˆAC
①求∠APC的度数；
②求四边形APCD的面积．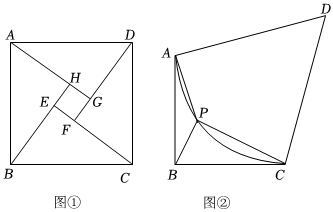
发布：2025/5/23 4:30:1组卷：429引用：1难度：0.3 -
2．已知AB是⊙O的直径，弦CD⊥AB，垂足为点H，点E在直径AB上（与A、B不重合），EH=AH，连接CE并延长与⊙O交于点F．
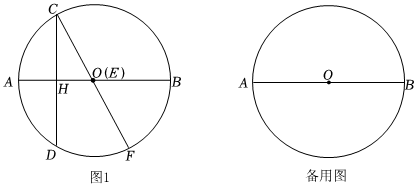
（1）如图1，当点E与点O重合时，求∠AOC的度数；
（2）连接AF交弦CD于点P，如果，求CEEF=43的值；DPCP
（3）当四边形ACOF是梯形时，且AB=6，求AE的长．发布：2025/5/23 5:0:2组卷：540引用：1难度：0.3 -
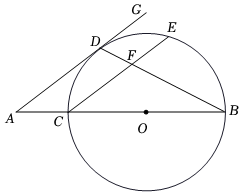3．如图，已知BC为⊙O的直径，点D为的中点，过点D作DG∥CE，交BC的延长线于点A，连接BD，交CE于点F．ˆCE
（1）求证：AD是⊙O的切线；
（2）若EF=3，CF=5，tan∠GDB=2，求AC的长．发布：2025/5/23 5:0:2组卷：1251引用：3难度：0.5
