平面直角坐标系中，抛物线y=-14x2+bx+c与直线KB交于点B（2，0），K（-12，-14），与y轴交于点C．
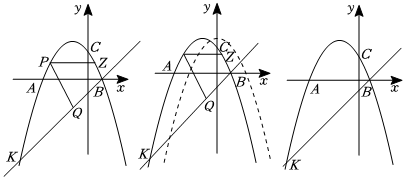
（1）求抛物线的函数表达式及顶点坐标；
（2）如图1，连接BC，点P是线段BK上方抛物线上的一个动点，过点P作PZ∥x轴交CB于点Z，过点P作PQ∥CB交直线KB于点Q，求655PQ+PZ的最大值及此时点P的坐标；
（3）如图2，在（2）的条件下，将该抛物线向下平移38个单位，向右平移3个单位，使得P点对应点P'．点S是新抛物线对称轴上一点，在平面上否存在一点N，使以P'、S、A、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
1
4
x
2
6
5
5
3
8
【考点】二次函数综合题．
【答案】（1），；
（2）最大值为，；
（3）或．
y
=
-
1
4
x
2
-
3
2
x
+
4
（
-
3
，
25
4
）
（2）
6
5
5
PQ
+
PZ
243
8
P
（
-
7
，
9
4
）
（3）
N
（
-
12
，
949
80
）
（
-
4
，-
15
8
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 15:0:2组卷：41引用：2难度：0.5
相似题
-
1．根据以下素材，探索完成任务．
如何设计喷水装置的高度？ 素材1 图1为某公园的圆形喷水池，图2是其示意图，O为水池中心，喷头A、B之间的距离为20米，喷射水柱呈抛物线形，水柱距水池中心7m处达到最高，高度为5m.水池中心处有一个圆柱形蓄水池，其底面直径CD为12m,高CF为1.8米． 
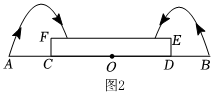
素材2 如图3，拟在圆柱形蓄水池中心处建一喷水装置OP （OP⊥CD），并从点P向四周喷射与图2中形状相同的抛物线形水柱，且满足以下条件：
①水柱的最高点与点P的高度差为0.8m；
②不能碰到图2中的水柱；
③落水点G，M的间距满足：GM：FM=2：7．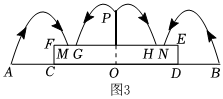
问题解决 任务1 确定水柱形状 在图2中以点O为坐标原点，水平方向为x轴建立直角坐标系，并求左边这条抛物线的函数表达式． 任务2 探究落水点位置 在建立的坐标系中，求落水点G的坐标． 任务3 拟定喷水装置的高度 求出喷水装置OP的高度． 发布：2025/5/23 4:30:1组卷：756引用：3难度：0.3 -
2．已知抛物线y=ax2+bx 经过点A（2，0）与点（-1，3）．
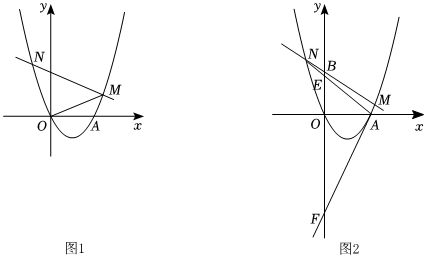
（1）求抛物线的解析式；
（2）直线y=kx+2与抛物线y=ax2+bx交于点M，N（点M，点N分别在第一、二象限）．
①如图1，连接OM，当∠OMN=45°时，求k的值；
②如图2，直线AN交y轴于点E，直线AM交y轴于点F，当时，求k的值．EF=57发布：2025/5/23 4:30:1组卷：298引用：1难度：0.2 -
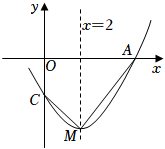3．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（5，0），与y轴交于点C，其对称轴为直线x=2，结合图象分析如下结论：①abc＞0；②b+3a＜0；③当x＞0时，y随x的增大而增大；④若一次函数y=kx+b（k≠0）的图象经过点A，则点E（k,b）在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a=．其中正确的有（ ）66发布：2025/5/23 5:0:2组卷：3755引用：22难度：0.2
