2022-2023学年湖南省益阳市南县立达中学高一（上）期中数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={1，2，3}，B={x|（x+1）（x-2）＜0，x∈Z}，则A∪B=（　　）

  A．{1}

  B．{1，2}

  C．{0，1，2，3}

  D．{-1，0，1，2，3}
  组卷：184引用：11难度：0.8

  解析

• 2．设集合A={x|x²-4≤0}，B={x|2x+a≤0}，且A∩B={x|-2≤x≤1}，则a=（　　）

  A．-4

  B．-2

  C．2

  D．4
  组卷：6313引用：57难度：0.8

  解析

• 3．下列各组函数中，表示同一函数的是（　　）

  A．f（x）=x与f（x）= x 2 x

  B．f（x）=x-1与 f （ x ） = （ x - 1 ） 2

  C．f（x）=x与 f （ x ） = 3 x 3

  D．f（x）=|x|与 f （ x ） = （ x ） 2
  组卷：97引用：8难度：0.9

  解析

• 4．设a∈R，则“a＞1”是“a²＞a”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：7837引用：112难度：0.7

  解析

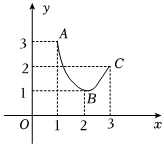• 5．已知函数y=f（x）的对应关系如表所示，函数y=g（x）的图象是如图所示的曲线ABC，则f[g（2）]的值为（　　）
  

  x	1	2	3
  f（x）	2	3	0

  A．3

  B．0

  C．1

  D．2
  组卷：39引用：8难度：0.7

  解析

• 6．若函数f（x）=x²-2（a-4）x+2在（-∞，3]上单调递减，则实数a的取值范围是（　　）

  A．a≥-7

  B．a≥7

  C．a≥3

  D．a≤-7
  组卷：28引用：4难度：0.8

  解析

• 7．已知f（x）=

  （ a - 3 ） x + a + 2 ， x ＜ 1 ，

  - a x 2 + x , x ≥ 1

  在（-∞，+∞）上单调递减，则实数a的取值范围为（　　）

  A．（0，3）

  B．[ 1 2 ，3）

  C．[ 2 3 ，3）

  D．[ 1 2 ， 2 3 ]
  组卷：589引用：6难度：0.6

  解析

四、解答题：本大题共6小题，满分70分，写出必要的文字说明、推演步骤．

• 21．为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y（单位：毫克/立方米）随着时间x（单位：天）变化的关系如下：当0≤x≤4时，y=

  8

  8

  -

  x

  ；当4＜x≤10时，y=4-

  1

  2

  x.若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知，当空气中净化剂的浓度不低于4（毫克/立方米）时，它才能起到净化空气的作用．
  （1）若一次喷洒4个单位的净化剂，则净化时间可达几天？
  （2）若第一次喷洒2个单位的净化剂，6天后再喷洒a（1≤a≤4）个单位的净化剂，要使接下来的4天中能够持续有效净化，试求a的最小值．
  组卷：130引用：7难度：0.6

  解析

• 22．已知命题：“∀x∈[-1，1]，都有不等式x²-x-m＜0成立”是真命题．
  （1）求实数m的取值集合B；
  （2）设不等式（x-3a）（x-a-2）＜0的解集为A，若x∈A是x∈B的充分不必要条件，求实数a的取值范围．
  组卷：92引用：7难度：0.7

  解析