2022-2023学年安徽省合肥市巢湖七中七年级(下)期中数学试卷
发布:2024/7/14 8:0:9
一、选择题(本大题共10小题,每小题4分,共40分)
-
1.下列说法中正确的是( )
组卷:487引用:2难度:0.7 -
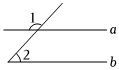 2.如图,a∥b,∠1=3∠2,则∠2的度数为( )组卷:21引用:1难度:0.5
2.如图,a∥b,∠1=3∠2,则∠2的度数为( )组卷:21引用:1难度:0.5 -
3.下列结论正确的是( )
组卷:126引用:1难度:0.9 -
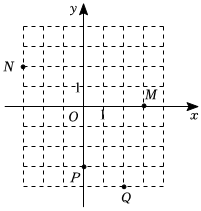 4.如图,在平面直角坐标系中有M、N、P、Q四个点,关于这四个点的坐标描述正确的是( )组卷:52引用:1难度:0.7
4.如图,在平面直角坐标系中有M、N、P、Q四个点,关于这四个点的坐标描述正确的是( )组卷:52引用:1难度:0.7 -
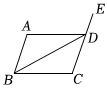 5.如图,在四边形ABCD中,连接BD,点E在CD的延长线上,下列命题正确的是( )组卷:50引用:1难度:0.5
5.如图,在四边形ABCD中,连接BD,点E在CD的延长线上,下列命题正确的是( )组卷:50引用:1难度:0.5 -
6.由x-
可以得到用x表示y的式子为( )y2=1组卷:96引用:2难度:0.8 -
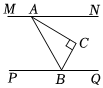 7.如图,MN∥PQ,将直角三角板ABC(其中∠BAC=30°)按图示放置,点A在MN上,点B在PQ上,若AC平分∠BAN,则∠CBQ的度数为( )组卷:125引用:2难度:0.5
7.如图,MN∥PQ,将直角三角板ABC(其中∠BAC=30°)按图示放置,点A在MN上,点B在PQ上,若AC平分∠BAN,则∠CBQ的度数为( )组卷:125引用:2难度:0.5
七.(本题满分12分)
-
22.定义:对于三个互不相等的负整数,若两两乘积的算术平方根都是整数,则称这三个数为“组合平方数”.例如:-1,-4,-9这三个数,
,(-1)×(-4)=2,(-1)×(-9)=3,其结果2,3,6都是整数,所以-1,-4,-9这三个数称为“组合平方数”.(-4)×(-9)=6
(1)-4,-16,-25这三个数是“组合平方数”吗?请说明理由;
(2)若三个数-3,m,-12是“组合平方数”,其中有两个数乘积的算术平方根为12,求m的值;
(3)写出一组含有-2的“组合平方数”.组卷:142引用:2难度:0.5
八.(本题满分14分
-
23.如图1,点E、F分别在直线AB、CD上,∠AEF的平分线交CD于G,且∠GEF=∠EGF.
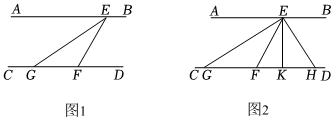
(1)判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,点H在射线FD上,∠FEH的平分线交CD于K.
①当∠FHE=50°时,求∠GEK的度数;
②若EH⊥EG,求证:.∠HEK=13∠BEK组卷:56引用:1难度:0.5


