2023-2024学年江西省宜春市丰城中学高二（上）入学数学试卷（8月份）

一．单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求。

• 1．设集合A={x∈Z|0＜x＜5}，B={x|a＜x＜5}，若A∩B={2，3，4}，则a的取值范围是（　　）

  A．（1，2）

  B．（1，2]

  C．[1，2）

  D．[1，2]
  组卷：142引用：2难度：0.8

  解析

• 2．已知cosα≠0，且4sin2α-3cos2α=3，则tanα=（　　）

  A． 3 5

  B． ± 3 5

  C． 3 4

  D． ± 3 4
  组卷：214引用：2难度：0.8

  解析

• 3．已知函数f（x）是定义在R上的偶函数，且在（-∞，0）上单调递增，设a=f（log₄5），

  b

  =

  f

  （

  log

  2

  1

  3

  ）

  ，c=f（0.2^0.5），则a,b,c的大小关系（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．b＜c＜a

  D．a＜b＜c
  组卷：203引用：7难度：0.6

  解析

• 4．已知f（x）的定义域是[-1，

  3

  2

  ]，则f（sin2x）的定义域为（　　）

  A． [ - 2 π 3 + kπ ， π 6 + kπ ] ，k∈Z	B． [ π 6 + kπ ， π 3 + kπ ] ，k∈Z
  C． [ - 2 π 3 + 2 kπ ， π 6 + 2 kπ ] ，k∈Z	D． [ π 6 + 2 kπ ， π 3 + 2 kπ ] ，k∈Z
  组卷：268引用：6难度：0.6

  解析

• 5．已知正数a、b满足

  1

  a

  +

  1

  b

  =1，则

  9

  a

  -

  1

  +

  4

  b

  -

  1

  的最小值是（　　）

  A．6

  B．12

  C．24

  D．36
  组卷：1860引用：4难度：0.5

  解析

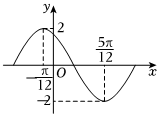• 6．函数y=Asin（ωx+φ）（A＞0）的一个周期内的图象如图所示，下列结论错误的是（　　）

  A．f（x）的解析式是 f （ x ） = 2 sin （ 2 x - π 3 ）

  B．函数f（x）的最小正周期是π

  C．函数f（x）的最大值是2

  D．函数f（x）的一个对称中心是 （ π 6 ， 0 ）
  组卷：399引用：6难度：0.6

  解析

• 7．某同学有一个形如圆台的水杯如图所示，已知圆台形水杯的母线长为6cm,上、下底面圆的半径分别为4cm和2cm.为了防烫和防滑，水杯配有一个杯套，包裹水杯

  2

  3

  高度以下的外壁和杯底，如图中阴影部分所示，则杯套的表面积为（不考虑水杯材质和杯套的厚度）（　　）
  

  A．24πcm2

  B．25πcm2

  C． 68 3 πc m 2

  D． 76 3 πc m 2
  组卷：182引用：5难度：0.8

  解析

四.解答题（第17题10分，第18-22题.每小题10分，共70分）

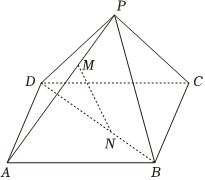• 21．如图，正四棱锥P-ABCD的侧棱长和底面边长均为13，M为侧棱PA上的点，且PM：MA=5：8．
  （1）在线段BD上是否存在一点N，使直线MN∥平面PBC？如果存在，求出BN：ND的值，如果不存在，请说明理由；
  （2）假设存在满足条件（1）的点N，求线段MN的长．
  组卷：75引用：4难度：0.5

  解析

• 22．在锐角△ABC中，记△ABC的内角A，B，C的对边分别为a,b,c,

  2

  bcos

  A

  =

  acos

  C

  +

  ccos

  A

  ，点O为△ABC的所在平面内一点，且满足

  （

  OA

  +

  OB

  ）

  •

  AB

  =

  （

  OB

  +

  OC

  ）

  •

  BC

  =

  0

  ．
  （1）若

  a

  =

  2

  ，求|AO|的值；
  （2）在（1）条件下，求

  |

  3

  OA

  +

  2

  OB

  +

  OC

  |

  的最小值．
  组卷：144引用：2难度：0.2

  解析